设数列{an}是公比为q的等比数列，Sn是它的前n项和．
(1)求证：数列{Sn}不是等比数列；
(2)数列{Sn}是等差数列吗？为什么？
小学课时特训系列答案科目：高中数学 来源： 题型：
下图是某市3月1日至14日的空气质量指数趋势图，空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气重度污染．某人随机选择3月1日至3月15日中的某一天到达该市，并停留2天．
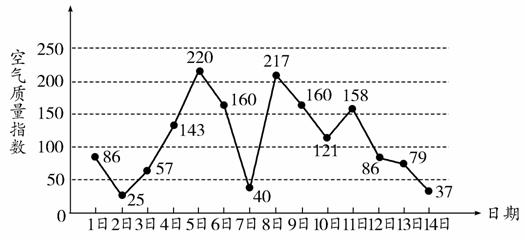
(1)求此人到达当日空气重度污染的概率；
(2)设X是此人停留期间空气质量优良的天数，求X的分布列与数学期望；
(3)由图判断从哪天开始连续三天的空气质量指数方差最大？(结论不要求证明)
查看答案和解析>>
科目：高中数学 来源： 题型：
类比“两角和与差的正弦公式”的形式，对于给定的两个函数：S(x)＝ax－a－x，C(x)＝ax＋a－x，其中a>0，且a≠1，下面正确的运算公式是( )
①S(x＋y)＝S(x)C(y)＋C(x)S(y)；
②S(x－y)＝S(x)C(y)－C(x)S(y)；
③2S(x＋y)＝S(x)C(y)＋C(x)S(y)；
④2S(x－y)＝S(x)C(y)－C(x)S(y)．
A．①② B．③④
C．①④ D．②③
查看答案和解析>>
科目：高中数学 来源： 题型：
以下是对命题“若两个正实数a1，a2满足a
＋a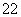
＝1，则a1＋a2≤
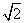”的证明过程：证明：构造函数f(x)＝(x－a1)2＋(x－a2)2＝2x2－2(a1＋a2)x＋1，因为对一切实数x，恒有f(x)≥0，所以Δ≤0，从而得4(a1＋a2)2－8≤0，所以a1＋a2≤.
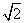根据上述证明方法，若n个正实数a1、a2、…、an满足a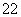＋a＋…＋a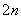
＝1时，你能得到的结论为____________________(不必证明)．
查看答案和解析>>
科目：高中数学 来源： 题型：
某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：
①sin213°＋cos217°－sin13°cos17°；
②sin215°＋cos215°－sin15°cos15°；
③sin218°＋cos212°－sin18°cos12°；
④sin2(－18°)＋cos248°－sin(－18°)cos48°；
⑤sin2(－25°)＋cos255°－sin(－25°)cos55°.
(1)试从上述五个式子中选择一个，求出这个常数；
(2)根据(1)的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．
查看答案和解析>>
科目：高中数学 来源： 题型：
在极坐标系中，已知点P(2，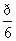
)，则过点P且平行于极轴的直线的方程是( )
A．ρsinθ＝1 B．ρsinθ＝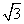
C．ρcosθ＝1 D．ρcosθ＝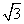
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
＋
i B.
<
，
<
，
<
，
.