练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    用数学归纳法证明下面的等式12－22＋32－42＋…＋(－1)n－1·n2＝(－1)n－1.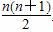


     (1)当n＝1时，左边＝12＝1，

    右边＝(－1)0·＝1，

    ∴原等式成立．

    (2)假设n＝k(k∈N＋，k≥1)时，等式成立，

    即有12－22＋32－42＋…＋(－1)k－1·k2

    ＝(－1)k－1.

    那么，当n＝k＋1时，则有

    12－22＋32－42＋…＋(－1)k－1·k2＋(－1)k·(k＋1)2

    ∴n＝k＋1时，等式也成立，

    由(1)(2)得对任意n∈N＋有

    12－22＋32－42＋…＋(－1)n－1·n2

    ＝.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知复数z的实部为－1，虚部为2，则 (i为虚数单位)在复平面内对应的点所在的象限为(　　)

    A．第一象限                                                 B．第二象限

    C．第三象限                                                 D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设数列{an}是公比为q的等比数列，Sn是它的前n项和．

    (1)求证：数列{Sn}不是等比数列；

    (2)数列{Sn}是等差数列吗？为什么？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某个命题与自然数n有关，若n＝k(k∈N*)时命题成立，则可推得当n＝k＋1时该命题也成立，现已知n＝5时，该命题不成立，那么可以推得(　　)

    A．n＝6时该命题不成立                               B．n＝6时该命题成立

    C．n＝4时该命题不成立                               D．n＝4时该命题成立

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，第n个图形是由正n＋2边形“扩展”而来的(n＝1,2,3，…)，则第n－2(n≥3，n∈N*)个图形共有________个顶点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正项数列{an}中，对于一切的n∈N*均有a≤an－an＋1成立．

    (1)证明：数列{an}中的任意一项都小于1；

    (2)探究an与的大小，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，AB是圆O的直径，点C在圆O上，延长BC到D使BC＝CD，过C作圆O的切线交AD于E.若AB＝6，ED＝2，则BC＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如下图，点D在⊙O的弦AB上移动，AB＝4，连接OD，过点D作OD的垂线交⊙O于点C，则CD的最大值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系的x轴的正半轴重合．设点O为坐标原点，直线l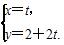：(参数t∈R)与曲线C的极坐标方程为ρcos2θ＝2sinθ.

    (1)求直线l与曲线C的普通方程；

    (2)设直线l与曲线C相交于A、B两点，证明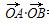：＝0.

    查看答案和解析>>

    同步练习册答案