
分析 (1)原不等式可化为|x-a|≤3,a-3≤x≤a+3.再根据不等f(x)≤3的解集为{x|-1≤x≤5},可得$\left\{\begin{array}{l}{a-3=-1}\\{a+3=5}\end{array}\right.$,从而求得a的值;
(2)由题意可得g(x)=|x-2|+|x+3|≥|(x-2)-(x+3)|=5,从而求得m的范围.
解答 解:(1)由题意,|x-a|≤3,∴a-3≤x≤a+3,
∵不等式f(x)≤3的解集为{x|-1≤x≤5},
∴$\left\{\begin{array}{l}{a-3=-1}\\{a+3=5}\end{array}\right.$,∴a=2;
(2)设g(x)=|x-2|+|x+3|≥|(x-2)-(x+3)|=5,当且仅当-3≤x≤2时,等号成立
∵存在实数x,使不等式f(x)+f(x+5)<m成立,
∴m>5.
点评 本题主要考查绝对值不等式的解法,带有绝对值的函数,体现了转化的数学思想,属于中档题.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | -1+i | C. | 1+2i | D. | 1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 28 | C. | 212 | D. | 215 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
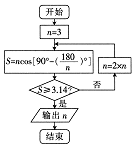 3世纪中期,魏晋时期的数学家刘徽首创“割圆术”,也就是在圆内割正多边形,求的近似值,刘徽容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失唉,当圆内接正多边形的边数无限增加时,多边形面积可无限近圆的面积,利用“割圆术”刘徽得到圆周率精确到小数点后两位的计算值3.14,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的n值为(参考数据:sin15°=0.259)( )
3世纪中期,魏晋时期的数学家刘徽首创“割圆术”,也就是在圆内割正多边形,求的近似值,刘徽容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失唉,当圆内接正多边形的边数无限增加时,多边形面积可无限近圆的面积,利用“割圆术”刘徽得到圆周率精确到小数点后两位的计算值3.14,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的n值为(参考数据:sin15°=0.259)( )| A. | 6 | B. | 12 | C. | 24 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com