
分析 f(x)在R上为奇函数,从而得到a2+a4=4,由此利用等差数列性质能求出S2015.
解答 解:∵f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,
∴$f(-x)=\frac{{2}^{-x}-1}{{2}^{-x}+1}$=$\frac{1-{2}^{x}}{1+{2}^{x}}$=-f(x),
∴f(x)在R上为奇函数,
∵f(a2-2)=-$\frac{\sqrt{3}}{2}$,f(a2014-2)=$\frac{\sqrt{3}}{2}$,
∴a2-2=-(a2014-2),即a2+a2014=4,
∴S2015=$\frac{2015}{2}({a}_{1}+{a}_{2015})$=$\frac{2015}{2}({a}_{2}+{a}_{2014})$=4030.
故答案为:4030.
点评 本题考查等差数列前2015项和的求法,是中档题,解题时要注意函数的奇偶性和等差数列性质的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| A型车 | B型车 | 限量 | |
| 车辆数 | x | y | 0≤x≤8,0≤y≤4 |
| 每天运物吨数 | 24x | 30y | 24x+30y≥180 |
| 每天往返成本费 | 320x | 504y | z |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 24 | C. | 36 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
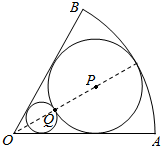 如图,在半径为常数r,圆心角为2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两条半径相切并与圆P外切的小圆Q.
如图,在半径为常数r,圆心角为2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两条半径相切并与圆P外切的小圆Q.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com