
分析 (1)令f′(x)=0得出x-lnx=0,再判断y=x-lnx的单调性得出最小值得出f′(x)>0,得出结论;
(2)求出右侧函数h(x)=$\frac{2{e}^{x-1}}{x{e}^{x}+1}$的最大值,再根据f(x)的单调性比较$\frac{f(x)}{e+1}$与hmax(x)的大小关系即可得出结论.
解答 解:(1)f′(x)=-$\frac{1}{{x}^{2}}$+$\frac{1}{x}$+$\frac{1-lnx}{{x}^{2}}$=$\frac{x-lnx}{{x}^{2}}$.
令ϕ(x)=x-lnx,则$ϕ'(x)=1-\frac{1}{x}=\frac{x-1}{x}$.
当x>1时,ϕ'(x)>0,ϕ(x)在区间(1,+∞)上单调递增;
当0<x<1时,ϕ'(x)<0,ϕ(x)在区间(0,1)上单调递减.
∴ϕ(x)在x=1处取得唯一的极小值,即为最小值.即ϕ(x)≥ϕ(1)=1>0,
∴f'(x)>0,
∴f(x)在区间(0,+∞)上是增函数.
(2)由(1)知,当x>1时,f(x)为增函数,故f(x)>f(1)=2,
故$\frac{f(x)}{e+1}>\frac{2}{e+1}$.
令$h(x)=\frac{{2{e^{x-1}}}}{{x{e^x}+1}}$,则$h'(x)=2\frac{{{e^{x-1}}(x{e^x}+1)-(x{e^x}+1)'{e^{x-1}}}}{{{{(x{e^x}+1)}^2}}}=\frac{{2{e^{x-1}}(1-{e^x})}}{{{{(x{e^x}+1)}^2}}}$,
∵x>1,∴1-ex<0.∴h'(x)<0,即h(x)在区间(1,+∞)上是减函数.
∴x>1时,$h(x)<h(1)=\frac{2}{e+1}$.
∴$\frac{f(x)}{e+1}>\frac{2}{e+1}>h(x)$,即$\frac{f(x)}{e+1}>\frac{{2{e^{x-1}}}}{{x{e^x}+1}}$.
点评 本题考查了导数与函数单调性的关系,函数最值的计算,属于中档题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:选择题
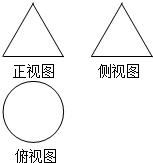 如图所示,一个空间几何体的正视图和侧视图都是边长为4的等边三角形,俯视图是一个圆,那么其体积为( )
如图所示,一个空间几何体的正视图和侧视图都是边长为4的等边三角形,俯视图是一个圆,那么其体积为( )| A. | $\frac{{4\sqrt{3}}}{3}π$ | B. | $\frac{{8\sqrt{3}}}{3}π$ | C. | $\frac{{\sqrt{3}}}{2}π$ | D. | 3π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com