
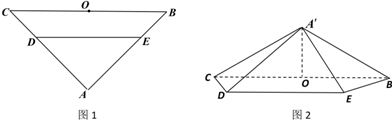
分析 (Ⅰ)利用线面垂直的判定定理证明A′O⊥平面BCDE.
(Ⅱ)利用等体积,求O到平面A′DE的距离.
解答 (Ⅰ)证明:在图1中,易得OC=3,AC=3$\sqrt{2}$,AD=2$\sqrt{2}$,
连结OD,OE,在△OCD中,
由余弦定理可得OD=$\sqrt{O{C}^{2}+C{D}^{2}-2OC•CDcos45°}$=$\sqrt{5}$
由翻折不变性可知A'D=2$\sqrt{2}$,
∴A'O2+OD2=A'D2,
∴A'O⊥OD.
同理可证A'O⊥OE,
又OD∩OE=O,
∴A'O⊥平面BCDE.
(Ⅱ)解:过D作DH⊥BC交OC于H,则DH=1,
∵DE=4,∴S△ODE=$\frac{1}{2}×4×1$=2.
∵S△A′DE=$\frac{1}{2}×4×\sqrt{8-4}$=4,
∴由等体积可得,O到平面A′DE的距离=$\frac{2×\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$.
点评 本题主要考查直线和平面垂直的判定定理以及点到平面距离的计算,要求熟练掌握相应的判定定理和体积的计算.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5377 | B. | -5377 | C. | 5375 | D. | -5375 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com