
| A. | $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | D. | 3$\overrightarrow{a}$+3$\overrightarrow{b}$+3$\overrightarrow{c}$ |
分析 由题意知$\overrightarrow{AG}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),从而化简可得.
解答 解:∵G是△ABC的重心,
∴$\overrightarrow{AG}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
∴$\overrightarrow{OG}$=$\overrightarrow{OA}$+$\overrightarrow{AG}$
=$\overrightarrow{OA}$+$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)
=$\overrightarrow{OA}$+$\frac{1}{3}$($\overrightarrow{OB}$-$\overrightarrow{OA}$+$\overrightarrow{OC}$-$\overrightarrow{OA}$)
=$\frac{1}{3}$($\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$)
=$\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$,
故选:C.
点评 本题考查了三角形重心的应用及向量的化简与运算.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2+x+1<0 | B. | ?x∈R,x2+x+1>0 | C. | ?x∈R,x2+x+1≥0 | D. | ?x∈R,x2+x+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
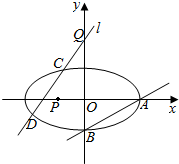 已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$ (a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(a,0)和B(0,-b)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.
已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$ (a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(a,0)和B(0,-b)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com