Question

11．以下五个关于圆锥曲线的命题中：
①双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$与椭圆$\frac{x^2}{49}+\frac{y^2}{24}=1$有相同的焦点；
②以抛物线的焦点弦（过焦点的直线截抛物线所得的线段）为直径的圆与抛物线的准线是相切的．
③设A、B为两个定点，k为常数，若|PA|-|PB|=k，则动点P的轨迹为双曲线；
④过抛物线y²=4x的焦点作直线与抛物线相交于A、B两点，则使它们的横坐标之和等于5的直线有且只有两条．
⑤过定圆C上一定点A作圆的动弦AB，O为原点，若$\overrightarrow{OP}=\frac{1}{2}（\overrightarrow{OA}+\overrightarrow{OB}）$，则动点P的轨迹为椭圆
其中真命题的序号为①②④（写出所有真命题的序号）

Answer 1

分析 ①根据椭圆和双曲线的c是否相同即可判断．
②根据抛物线的性质和定义进行判断．
③根据双曲线的定义进行判断．
④根据抛物线的定义和性质进行判断．
⑤根据圆锥曲线的根据方程进行判断．

解答 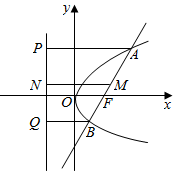解：①由$\frac{x^2}{16}-\frac{y^2}{9}=1$得a²=16，b²=9，则c²=16+9=25，即c=5，
由椭圆$\frac{x^2}{49}+\frac{y^2}{24}=1$得a²=49，b²=24，则c²=49-24=25，即c=5，则双曲线和椭圆有相同的焦点，故①正确，
②不妨设抛物线方程为y²=2px（p＞0），
取AB的中点M，分别过A、B、M作准线的垂线AP、BQ、MN，垂足分别为P、Q、N，如图所示：
由抛物线的定义可知，|AP|=|AF|，|BQ|=|BF|，
在直角梯形APQB中，|MN|=$\frac{1}{2}$（|AP|+|BQ|）=$\frac{1}{2}$（|AF|+|BF|）=$\frac{1}{2}$|AB|，
故圆心M到准线的距离等于半径，
∴以AB为直径的圆与抛物线的准线相切，故②正确，
③平面内与两个定点F₁，F₂的距离的差的绝对值等于常数k（k＜|F₁F₂|）的点的轨迹叫做双曲线，
当0＜k＜|AB|时是双曲线的一支，当k=|AB|时，表示射线，∴故③不正确；
④过抛物线y²=4x的焦点F（1，0）作直线l与抛物线相交于A、B两点，
当直线l的斜率不存在时，横坐标之和等于2，不合题意；
当直线l的斜率为0时，只有一个交点，不合题意；
∴设直线l的斜率为k（k≠0），则直线l为y=k（x-1），
代入抛物线y²=4x得，k²x²-2（k²+2）x+k²=0；
∵A、B两点的横坐标之和等于5，
∴$\frac{2（{k}^{2}+2）}{{k}^{2}}$=5，解得k²=$\frac{4}{3}$，
∴这样的直线有且仅有两条．故④正确，
⑤设定圆C的方程为（x-a）²+（x-b）²=r²，其上定点A（x₀，y₀），设B（a+rcosθ，b+rsinθ），P（x，y），
由$\overrightarrow{OP}$=$\frac{1}{2}$（$\overrightarrow{OA}$+$\overrightarrow{OB}$）得$\left\{\begin{array}{l}x=\frac{{x}_{0}+a+rcosθ}{2}\\ y=\frac{{y}_{0}+b+rsinθ}{2}\end{array}\right.$，消掉参数θ，得：（2x-x₀-a）²+（2y-y₀-b）²=r²，即动点P的轨迹为圆，故⑤错误；
故答案为：①②④

点评 本题考查命题的真假判断与应用，综合考查椭圆、双曲线的定义与标准方程、几何性质的应用，考查椭圆的参数方程的应用，属于难题．