
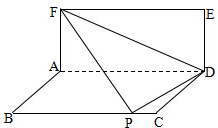
 已知两矩形ABCD与ADEF所在的平面互相垂直,AB=1,若将△DEF沿直线FD翻折,使得点E落在边BC上(即点P),则当AD取最小值时,边AF的长是$\sqrt{2}$;此时四面体F-ADP的外接球的半径是$\frac{\sqrt{6}}{2}$.
已知两矩形ABCD与ADEF所在的平面互相垂直,AB=1,若将△DEF沿直线FD翻折,使得点E落在边BC上(即点P),则当AD取最小值时,边AF的长是$\sqrt{2}$;此时四面体F-ADP的外接球的半径是$\frac{\sqrt{6}}{2}$. 分析 由已知中矩形ABCD与矩形ADEF所在的平面互相垂直,将△DEF沿FD翻折,翻折后的点E恰与BC上的点P重合.设AB=1,FA=x(x>1),AD=y,我们利用勾股定理分别求出BP,PC,根据BC=BP+PC,可以得到 x,y的关系式,利用换元法结合二次函数的性质,可得答案.四面体F-ADP的外接球的球心为DF的中点,即可求出四面体F-ADP的外接球的半径.
解答 解:设FA=x(x>1),AD=y,
∵矩形ABCD与矩形ADEF所在的平面互相垂直,AB=1,FA=x(x>1),AD=y,
∴FE=FP=AD=BC=y,AB=DC=1,FA=DE=DP=x
在Rt△DCP中,PC=$\sqrt{{x}^{2}-1}$
在Rt△FAP中,AP=$\sqrt{{y}^{2}-{x}^{2}}$
在Rt△ABP中,BP=$\sqrt{{y}^{2}-{x}^{2}-1}$
∵BC=BP+PC=$\sqrt{{y}^{2}-{x}^{2}-1}$+$\sqrt{{x}^{2}-1}$=y
整理得y2=$\frac{{x}^{4}}{{x}^{2}-1}$,令x2=$\frac{1}{t}$
则y2=$\frac{1}{-{t}^{2}+t}$,
则当t=$\frac{1}{2}$,即x=$\sqrt{2}$时,y取最小值2.
四面体F-ADP的外接球的球心为DF的中点,DF=$\sqrt{2+4}$=$\sqrt{6}$,四面体F-ADP的外接球的半径是$\frac{\sqrt{6}}{2}$.
故答案为:$\sqrt{2}$,$\frac{\sqrt{6}}{2}$.
点评 本题考查的知识点是空间两点之间的距离计算,由于本题是几何与代数知识的综合应用,运算量比较大,而且得到的x,y的关系比较复杂,因此要用换元法,简单表达式.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $\frac{1}{2}$ | C. | ±2 | D. | ±$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | (0,1] | C. | [1,+∞) | D. | (-∞,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 相关人员数 | 抽取人数 | |
| 环保专家 | 24 | x |
| 海洋生物专家 | 48 | 4 |
| 油气专家 | 36 | y |
| 重度污染 | 轻度污染 | 合计 | |
| 身体健康 | 30 | A | 50 |
| 身体不健康 | B | 10 | 60 |
| 合计 | C | D | E |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 0.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com