
分析 (1)根据二项式展开式中各项系数和求出n的值,再计算展开式中二项式系数的最大项;
(2)利用二项展开式的通项公式,即可求出展开式的常数项.
解答 解:(1)因为二项式(3x-$\frac{1}{\root{3}{x}}$)n的展开式中各项系数之和为256,
所以(3-1)n=256,
解得n=8;…(3分)
则该展开式中共有9项,第5项系数最大;
二项式系数最大项为T5=${C}_{8}^{4}$•(3x)8-4•${(\root{3}{x})}^{4}$=5670${x}^{\frac{8}{3}}$;…(6分)
(2)二项展开式的通项公式为
Tr+1=${C}_{8}^{r}$•(3x)8-r•${(\root{3}{x})}^{r}$=${C}_{8}^{r}$•38-r•${x}^{8-\frac{4}{3}r}$,
令8-$\frac{4}{3}$r=0,解得r=6;…(10分)
因此展开式的常数项为
T7=${C}_{8}^{6}$•38-6=252.…(12分)
点评 本题考查了二项式展开式中各项系数和以及展开式中二项式系数、通项公式的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
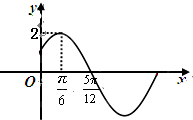 已知函数f(x)=Asin(ωx+φ)(φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25 | B. | 125 | C. | 120 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
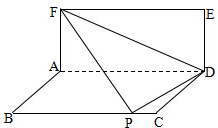 已知两矩形ABCD与ADEF所在的平面互相垂直,AB=1,若将△DEF沿直线FD翻折,使得点E落在边BC上(即点P),则当AD取最小值时,边AF的长是$\sqrt{2}$;此时四面体F-ADP的外接球的半径是$\frac{\sqrt{6}}{2}$.
已知两矩形ABCD与ADEF所在的平面互相垂直,AB=1,若将△DEF沿直线FD翻折,使得点E落在边BC上(即点P),则当AD取最小值时,边AF的长是$\sqrt{2}$;此时四面体F-ADP的外接球的半径是$\frac{\sqrt{6}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com