
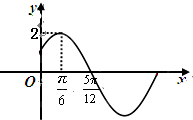
 已知函数f(x)=Asin(ωx+φ)(φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(φ|<$\frac{π}{2}$)的部分图象如图所示.分析 (1)由题意求出A,T,利用周期公式求出ω,利用当x=$\frac{π}{6}$时取得最大值2,求出φ,得到函数的解析式,即可得解.
(2)由$\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{3π}{2}+2kπ$,k∈Z即可解得f(x)的单调减区间.
(3)由$x∈[0,\frac{π}{12}]$,可求2x+$\frac{π}{6}$的范围,利用正弦函数的图象和性质即可得解最大值.
解答 (本题满分为14分)
解:(1)∵A>0,ω>0,
∴由图象知A=2,…(1分)
由于f(x)的最小正周期$T=4×(\frac{5π}{12}-\frac{π}{6})=π$,故$ω=\frac{2π}{T}=2$,…(3分)
将点$(\frac{π}{6},2)$代入f(x)的解析式得:$sin(\frac{π}{3}+φ)=1$,
又$|φ|<\frac{π}{2}$,
可得:$φ=\frac{π}{6}$,…(5分)
故函数f(x)的解析式为:$f(x)=2sin(2x+\frac{π}{6})$.…(6分)
(2)由$\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{3π}{2}+2kπ$,…(8分)
得$\frac{π}{6}+kπ≤x≤\frac{2π}{3}+kπ$,k∈Z,
所以减区间为:$[{\frac{π}{6}+kπ,\frac{2π}{3}+kπ}]({k∈Z})$.…(10分)
(3)当$x∈[0,\frac{π}{12}]$时,可得:$2x+\frac{π}{6}∈[\frac{π}{6},\frac{π}{3}]$,…(12分)
所以当$2x+\frac{π}{6}=\frac{π}{3}$,即$x=\frac{π}{12}$时,f(x)的最大值$\sqrt{3}$.…(14分)
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象和性质,解题时要注意函数的周期的求法,考查计算能力,是常考题型,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $A_3^3$•$A_4^3$ | B. | $A_3^3$•$A_3^3$ | C. | $A_4^3$•$A_4^3$ | D. | 2$A_3^3$•$A_3^3$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | -$\frac{π}{3}$ | D. | -$\frac{π}{6}$或$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 相关人员数 | 抽取人数 | |
| 环保专家 | 24 | x |
| 海洋生物专家 | 48 | 4 |
| 油气专家 | 36 | y |
| 重度污染 | 轻度污染 | 合计 | |
| 身体健康 | 30 | A | 50 |
| 身体不健康 | B | 10 | 60 |
| 合计 | C | D | E |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 0.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com