
已知在直角坐标系xOy中,直线l的参数方程为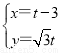 ,(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
,(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)设点P是曲线C上的一个动点,求它到直线l的距离d的取值范围.
科目:高中数学 来源:2015届河南省名校高三上学期期中文科数学试卷(解析版) 题型:选择题
已知函数 若
若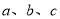 互不相等,且
互不相等,且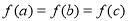 ,则
,则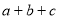 的取值范围是( )
的取值范围是( )
A.(1,2014) B.(1,2015) C.(2,2015) D.[2,2015]
查看答案和解析>>
科目:高中数学 来源:2015届河南省名校高三上学期期中文科数学试卷(解析版) 题型:选择题
设f(x)是定义在R上的奇函数,当 时,f(x)=x
时,f(x)=x (e为自然对数的底数),则
(e为自然对数的底数),则 的值为 ( )
的值为 ( )
A.ln6+6 B. ln6-6 C. -ln6+6 D.-ln6-6
查看答案和解析>>
科目:高中数学 来源:2015届河南省八校高三上学期第一次联考理科数学试卷(解析版) 题型:解答题
现有4个人去参加娱乐活动,该活动有甲、乙两个游戏可供参加者选择,为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏。
(Ⅰ)求这4个人中恰有2人去参加甲游戏的概率;
(Ⅱ)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(Ⅲ)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望 .
.
查看答案和解析>>
科目:高中数学 来源:2015届河南省八校高三上学期第一次联考理科数学试卷(解析版) 题型:选择题
已知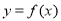 为R上的连续可导函数,当x≠0时
为R上的连续可导函数,当x≠0时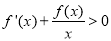 ,则函数
,则函数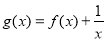 的零点个数为( )
的零点个数为( )
A.1 B.2 C.0 D.0或2
查看答案和解析>>
科目:高中数学 来源:2015届河南省八校高三上学期第一次联考文科数学试卷(解析版) 题型:解答题
抛掷一枚质地不均匀的骰子,出现向上点数为1,2,3,4, 5, 6的概率依次记为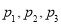 ,
,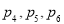 ,经统计发现,数列
,经统计发现,数列 恰好构成等差数列,且
恰好构成等差数列,且 是
是 的3倍.
的3倍.
(Ⅰ)求数列 的通项供式;
的通项供式;
(Ⅱ)甲、乙两人用这枚骰子玩游戏,并规定:掷一次骰子后,若向上点数为奇数,则甲获胜,否者乙获胜,请问这样的规则对甲、乙二人是否公平,请说明理由;
(Ⅲ)甲、乙丙三人用这枚骰子玩游戏,根据掷一次后向上的点数决定胜出者,并制定了公平的游戏方案,试在下面的表格中列举出两种可能的方案(不必证明)
方案序号 | 甲胜出对应点数 | 乙胜出对应点数 | 丙胜出对应点数 |
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com