
| A. | (-∞,-2012) | B. | (-2016,-2012) | C. | (-∞,-2016) | D. | (-2016,0) |
分析 构造函数F(x)=x2f(x),根据导数求出函数的单调区间,再由(x+2014)2f(x+2014)+4f(-2)<0转化为F(x+2014)<-F(-2)=F(2),解得即可.
解答 解:由2f(x)+xf′(x)>x2,(x>0);
得:2xf(x)+x2f′(x)>x3
即[x2f(x)]′>x3>0;
令F(x)=x2f(x);
则当x>0时,F'(x)>0,即F(x)在(0,+∞)上是增函数,
∵f(x)为奇函数,
∴F(x)=x2f(x)为奇函数,
∴F(x)在(-∞,0)上是增函数,
∴F(x+2014)=(x+2014)2f(x+2014),F(-2)=4f(-2);
即不等式等价为F(x+2014)+F(-2)<0;
即F(x+2014)<-F(-2)=F(2),
∴x+2014<2,∴x<-2012;
∴原不等式的解集是(-∞,-2012).
故选:A.
点评 本题考查函数的单调性与导数的关系,两个函数乘积的导数的求法,而构造函数是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图所示的几何体中,四边形ABCD为等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.
如图所示的几何体中,四边形ABCD为等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 在区间(-2,1)上f(x)是增函数 | B. | 在(1,3)上f(x)是减函数 | ||
| C. | 当x=4时,f(x)取极大值 | D. | 在(4,5)上f(x)是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,0] | B. | [0,2] | C. | [-2,2] | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
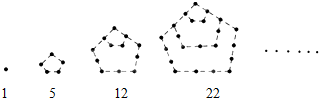 如图中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作a1=1,第2个五角形数记作a2=5,第3个五角形数记作a3=12,第4个五角形数记作a4=22,…,若按此规律继续下去,则an=$\frac{{3{n^2}-n}}{2}$.
如图中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作a1=1,第2个五角形数记作a2=5,第3个五角形数记作a3=12,第4个五角形数记作a4=22,…,若按此规律继续下去,则an=$\frac{{3{n^2}-n}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{2}{13}$ | C. | $\frac{11}{3}$ | D. | $\frac{1}{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com