
分析 (1)把a的值代入A中不等式,求出解确定出A即可;
(2)求出B中不等式的解集确定出B,根据A与B的交集为A,得到A为B的子集,确定出a的范围即可.
解答 解:(1)把a=-1代入A中不等式得:|x+1|<2,
变形得:-2<x+1<2,
解得:-3<x<1,即A={x|-3<x<1};
(2)∵A∩B=A,A={x||x-a|<2}={x|a-2<x<a+2},B={x|$\frac{1}{4}$<2x<8}={x|-2<x<3},
∴A⊆B,
∴$\left\{\begin{array}{l}{a-2≥-2}\\{a+2≤3}\end{array}\right.$,
解得:0≤a≤1.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2012) | B. | (-2016,-2012) | C. | (-∞,-2016) | D. | (-2016,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
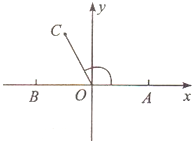 在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.
在如图所示的平面直角坐标系中,已知点A(1,0)和点B(-1,0),|$\overrightarrow{OC}$|=1,且∠AOC=x,其中O为坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
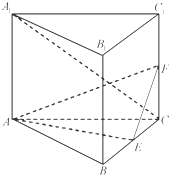 如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,AA1=$\sqrt{2}$,E,F分别是BC,CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,AA1=$\sqrt{2}$,E,F分别是BC,CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:解答题
已知函数 ,函数
,函数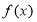 与
与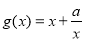 有相同极值点.
有相同极值点.
(1)求函数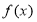 的最大值;
的最大值;
(2)求实数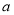 的值;
的值;
(3)若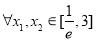 ,不等式
,不等式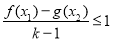 恒成立,求实数
恒成立,求实数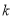 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届安徽合肥一中高三上学期月考一数学(文)试卷(解析版) 题型:选择题
设函数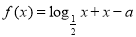 ,则“
,则“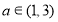 ”是“函数
”是“函数 在
在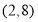 上存在零点”的( )
上存在零点”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(文)试卷(解析版) 题型:选择题
若不等式 表示的平面区域为
表示的平面区域为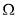 ,
,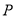 、
、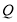 均为
均为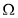 内一点,
内一点,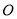 为坐标原点,
为坐标原点, ,则下列判断正确的是( )
,则下列判断正确的是( )
A.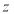 的最小值为
的最小值为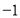 B.
B.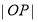 的最小值为
的最小值为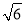
C.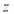 的最大值为
的最大值为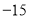 D.
D.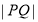 的最大值为
的最大值为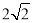
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com