

| A. | 在区间(-2,1)上f(x)是增函数 | B. | 在(1,3)上f(x)是减函数 | ||
| C. | 当x=4时,f(x)取极大值 | D. | 在(4,5)上f(x)是增函数 |
分析 由于f′(x)≥0⇒函数f(x)单调递增;f′(x)≤0⇒单调f(x)单调递减,观察f′(x)的图象可知,通过观察f′(x)的符号判定函数的单调性即可.
解答 解:由于f′(x)≥0⇒函数f(x)单调递增;f′(x)≤0⇒单调f(x)单调递减
观察f′(x)的图象可知,
当x∈(-2,1)时,函数先递减,后递增,故A错误
当x∈(1,3)时,函数先增后减,故B错误
当x∈(4,5)时函数递增,故D正确
由函数的图象可知函数在x=4处取得函数的极小值,故C错误
故选:D.
点评 本题主要考查了导数的应用:通过导数的符号判定函数单调性,要注意不能直接看导函数的单调性,而是通过导函数的正负判定原函数的单调性.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | k-1 | B. | k | C. | k+1 | D. | k2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2012) | B. | (-2016,-2012) | C. | (-∞,-2016) | D. | (-2016,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
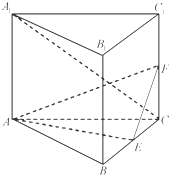 如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,AA1=$\sqrt{2}$,E,F分别是BC,CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,AA1=$\sqrt{2}$,E,F分别是BC,CC1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com