
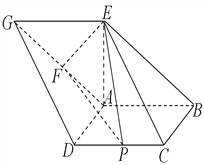
【题目】如图,已知四边形![]() 和
和![]() 均为平行四边形,点
均为平行四边形,点![]() 在平面
在平面![]() 内的射影恰好为点
内的射影恰好为点![]() ,以
,以![]() 为直径的圆经过点
为直径的圆经过点![]() ,
, ![]() ,
, ![]() 的中点为
的中点为![]() ,
, ![]() 的中点为
的中点为![]() ,且
,且![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求几何体![]() 的体积.
的体积.
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球,再从装有1个蓝球与2个白球的袋中任意摸出1个球,根据摸出4个球中红球与蓝球的个数,设一、二、三等奖如下:
奖级 | 摸出红、蓝球个数 | 获奖金额 |
一等奖 | 3红1蓝 | 200元 |
二等奖 | 3红0蓝 | 50元 |
三等奖 | 2红1蓝 | 10元 |
其余情况无奖且每次摸奖最多只能获得一个奖级.
(1)求一次摸奖恰好摸到1个红球的概率;
(2)求摸奖者在一次摸奖中获奖金额X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校组织“中国诗词”竞赛,在“风险答题”的环节中,共为选手准备了![]() 三类不同的题目,选手每答对一个
三类不同的题目,选手每答对一个![]() 类、
类、![]() 类或
类或![]() 类的题目,将分别得到
类的题目,将分别得到![]() 分,
分, ![]() 分,
分, ![]() 分,但如果答错,则相应要扣去
分,但如果答错,则相应要扣去![]() 分,
分, ![]() 分,
分, ![]() 分,根据平时训练经验,选手甲答对
分,根据平时训练经验,选手甲答对![]() 类、
类、![]() 类或
类或![]() 类的题目的概率分别为
类的题目的概率分别为![]() 、
、![]() 、
、![]() ,若要每一次答题的均分更大一些,则选手甲应选择的题目类型应为_________.(填
,若要每一次答题的均分更大一些,则选手甲应选择的题目类型应为_________.(填![]() ,
, ![]() 或
或![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年时红军长征胜利80周年,某市电视台举办纪念红军长征胜利80周年知识问答,宣传长征精神.首先在甲、乙、丙、丁四个不同的公园进行支持签名活动,其次在各公园签名的人中按分层抽样的方式抽取10名幸运之星,每人获得一个纪念品,其数据表格如下:
公园 | 甲 | 乙 | 丙 | 丁 |
获得签名人数 | 45 | 60 | 30 | 15 |
(Ⅰ)求此活动中各公园幸运之星的人数;
(Ⅱ)从乙和丙公园的幸运之星中任选两人接受电视台记者的采访,求这两人均来自乙公园的概率;
(Ⅲ)电视台记者对乙公园的签名人进行了是否有兴趣研究“红军长征”历史的问卷调查,统计结果如下(单位:人):
有兴趣 | 无兴趣 | 合计 | |
男 | 25 | 5 | 30 |
女 | 15 | 15 | 30 |
合计 | 40 | 20 | 60 |
据此判断能否在犯错误的概率不超过0.01的前提下认为有兴趣研究“红军长征”历史与性别有关.
临界值表:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式: 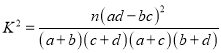 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某居民区的物业部门每月向居民收取卫生费,计费方法如下:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费,并画出程序框图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中是假命题的是
A. “昆虫都是6条腿,竹节虫是昆虫,所以竹节虫有6条腿”此推理属于演绎推理.
B. “在平面中,对于三条不同的直线![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,
, ![]() 则
则![]() ,将此结论放到空间中也成立” 此推理属于合情推理.
,将此结论放到空间中也成立” 此推理属于合情推理.
C. “![]() ”是“函数
”是“函数![]()
![]() 存在极值”的必要不充分条件.
存在极值”的必要不充分条件.
D. 若![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形,
是菱形, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() 交于点
交于点![]() ,
, ![]() 是
是![]() 上任意一点.
上任意一点.
(1)求证: ![]() ;
;
(2)已知二面角![]() 的余弦值为
的余弦值为![]() ,若
,若![]() 为
为![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com