
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)讨论方程![]() 的实数根的情况.
的实数根的情况.
【答案】(1)![]() (2)当
(2)当![]() 时,方程有两个实数根;当
时,方程有两个实数根;当![]() 时,方程无实数根.
时,方程无实数根.
【解析】试题分析: (1)求出![]() ,利用两直线垂直,求出
,利用两直线垂直,求出![]() 的值; (2)设
的值; (2)设![]() ,利用单调性求出
,利用单调性求出![]() , 分类讨论:
, 分类讨论: ![]() ,得出结果.
,得出结果.
试题解析:(1)依题意,得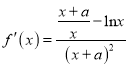 ,
,
所以![]() ,
,
又由曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,可得
垂直,可得![]() ,
,
所以![]() ,解得
,解得![]() ;
;
(2)方程![]() ,即
,即![]() .
.
当![]() 时,得
时,得![]() ,解得
,解得![]() ,
,
当![]() 时,解得
时,解得![]() .但是
.但是![]() ,即
,即![]() ,所以
,所以![]() 时,方程无实数根.
时,方程无实数根.
令![]() ,则
,则![]() ,
,
故当![]() 时,
时, ![]() 是单调递增函数;当
是单调递增函数;当![]() 时,
时, ![]() 是单调递减函数,
是单调递减函数,
所以![]() .
.
当![]() 时,由
时,由![]() ,得
,得![]() .
.
又![]() ,令
,令![]() ,则
,则![]() 在区间
在区间![]() 上
上![]() ,故
,故![]() 为增函数,所以
为增函数,所以![]() ,即
,即![]() ,所以
,所以![]() .
.
![]() ,故当
,故当![]() 时,方程有两个实数根;当
时,方程有两个实数根;当![]() 时,方程无实数根.
时,方程无实数根.
点睛: 本题主要考查了导数的几何意义以及函数零点的个数,属于中档题.
【一题多解】在(2)中,由![]() 有
有![]() ,转化为函数
,转化为函数![]() 与
与![]() 图象交点的个数,当
图象交点的个数,当![]() 与
与![]() 相切时,切点为
相切时,切点为![]() ,又
,又![]() ,所以此时无零点;由图象知,当
,所以此时无零点;由图象知,当![]() 时图象有两个交点,即有两个零点,
时图象有两个交点,即有两个零点, ![]() ,图象没有交点,无零点,综上讨论,得出结论:
,图象没有交点,无零点,综上讨论,得出结论: ![]() 有两个实数根,
有两个实数根, ![]() 无实数根.
无实数根.


科目:高中数学 来源: 题型:
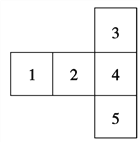
【题目】编号为A,B,C,D,E的5个小球放在如图所示的5个盒子里,要求每个盒子只能放1个小球,且A球不能放在1,2号盒子里,B球必须放在与A球相邻的盒子中,求不同的放法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,与
两点,与![]() 轴,
轴, ![]() 轴分别相交于点
轴分别相交于点![]() 和点
和点![]() ,且
,且![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,
轴的对称点, ![]() 的延长线交椭圆于点
的延长线交椭圆于点![]() ,过点
,过点![]() 分别做
分别做![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() .
.
(1) 若椭圆![]() 的左、右焦点与其短轴的一个端点是正三角形的三个顶点,点
的左、右焦点与其短轴的一个端点是正三角形的三个顶点,点![]() 在椭圆
在椭圆![]() 上,求椭圆
上,求椭圆![]() 的方程;
的方程;
(2)当![]() 时,若点
时,若点![]() 平分线段
平分线段![]() ,求椭圆
,求椭圆![]() 的离心率.
的离心率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某土特产销售总公司为了解其经营状况,调查了其下属各分公司月销售额和利润,得到数据如下表:
分公司名称 | 雅雨 | 雅鱼 | 雅女 | 雅竹 | 雅茶 |
月销售额 | 3 | 5 | 6 | 7 | 9 |
月利润额 | 2 | 3 | 3 | 4 | 5 |
在统计中发现月销售额![]() 和月利润额
和月利润额![]() 具有线性相关关系.
具有线性相关关系.
(1)根据如下的参考公式与参考数据,求月利润额![]() 与月销售额
与月销售额![]() 之间的线性回归方程;
之间的线性回归方程;
(2)若该总公司还有一个分公司“雅果”月销售额为10万元,试估计它的月利润额是多少?
(参考公式: 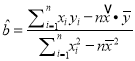 ,
, ![]() ,其中:
,其中: ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,以椭圆的四个顶点为顶点的四边形的面积为8.
,以椭圆的四个顶点为顶点的四边形的面积为8.
(Ⅰ)求椭圆![]() 的方程;
的方程;
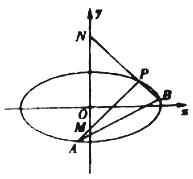
(Ⅱ)如图,斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,点
两点,点![]() 在直线
在直线![]() 的左上方.若
的左上方.若![]() ,且直线
,且直线![]() ,
, ![]() 分别与
分别与![]() 轴交于
轴交于![]() ,
, ![]() 点,求线段
点,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
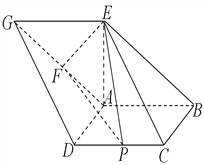
【题目】如图,已知四边形![]() 和
和![]() 均为平行四边形,点
均为平行四边形,点![]() 在平面
在平面![]() 内的射影恰好为点
内的射影恰好为点![]() ,以
,以![]() 为直径的圆经过点
为直径的圆经过点![]() ,
, ![]() ,
, ![]() 的中点为
的中点为![]() ,
, ![]() 的中点为
的中点为![]() ,且
,且![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地最近十年粮食需求量逐年上升,下表是部分统计数据:
年份 | 2006 | 2008 | 2010 | 2012 | 2014 |
需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
(1)利用所给数据求年需求量与年份之间的回归方程![]() =
=![]() x+
x+![]() ;
;
(2)利用(1)中所求出的直线方程预测该地2018年的粮食需求量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)用定义证明函数![]() 在
在![]() 上是增函数;
上是增函数;
(2)探究是否存在实数![]() ,使得函数
,使得函数![]() 为奇函数?若存在,求出
为奇函数?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)在(2)的条件下,解不等式![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com