
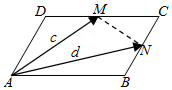
 (1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知$\overrightarrow{AM}=\overrightarrow{c}$、$\overrightarrow{AN}=\overrightarrow{d}$,试用$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知$\overrightarrow{AM}=\overrightarrow{c}$、$\overrightarrow{AN}=\overrightarrow{d}$,试用$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.分析 (1)用$\overrightarrow{AB},\overrightarrow{AD}$表示出$\overrightarrow{c},\overrightarrow{d}$,解方程组得出$\overrightarrow{AB},\overrightarrow{AD}$;
(2)根据向量加法的平行四边形法则得出$\overrightarrow{AP}+\overrightarrow{AS}=2\overrightarrow{AQ}=\overrightarrow{AB}+\overrightarrow{AC}$.
解答 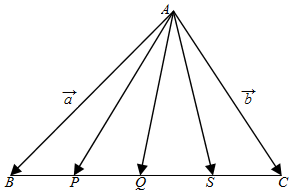 解:(1)∵$\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{DM}$=$\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}$,$\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}$=$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$
解:(1)∵$\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{DM}$=$\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}$,$\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}$=$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$
∴$\left\{\begin{array}{l}{\overrightarrow{c}=\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}}\\{\overrightarrow{d}=\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}}\end{array}\right.$,解得$\overrightarrow{AB}=-\frac{2}{3}\overrightarrow{c}+\frac{4}{3}\overrightarrow{d}$,$\overrightarrow{AD}=\frac{4}{3}\overrightarrow{c}-\frac{2}{3}\overrightarrow{d}$.
(2)∵P,Q,S为线段BC的四等分点,
∴Q是BC的中点,也是PS的中点.
∴$\overrightarrow{AQ}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$=$\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$,
$\overrightarrow{AP}+\overrightarrow{AS}$=2$\overrightarrow{AQ}$=$\overrightarrow{a}+\overrightarrow{b}$,
∴$\overrightarrow{AP}+\overrightarrow{AQ}+\overrightarrow{AS}$=$\frac{3}{2}\overrightarrow{a}+\frac{3}{2}\overrightarrow{b}$.
点评 本题考查了平面向量的基本定理,向量加法的几何意义,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{15}{16}$) | B. | ($\frac{15}{16}$,1) | C. | (1,$\frac{16}{15}$) | D. | (1,$\frac{5}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2$\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
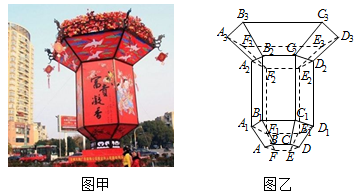 某地为了庆祝国庆66周年,现计划在城市中心广场搭建一个巨型花篮(如图甲).其中主体框梨(如图乙)准备用钢材焊接而成,具体设计方案如下:①上、中、下三部分依次由正六棱台、正六棱柱、正六棱台组成;②这三个几何体的侧面用于张贴宣传城市风光的图片,且侧面积之和为108m2;③BC:B1C1:B3C3=1:2:4,∠BB1C1=∠B2B3C3=α,且sinα=$\frac{4}{5}$,设BC=xm,B1B2=ym.
某地为了庆祝国庆66周年,现计划在城市中心广场搭建一个巨型花篮(如图甲).其中主体框梨(如图乙)准备用钢材焊接而成,具体设计方案如下:①上、中、下三部分依次由正六棱台、正六棱柱、正六棱台组成;②这三个几何体的侧面用于张贴宣传城市风光的图片,且侧面积之和为108m2;③BC:B1C1:B3C3=1:2:4,∠BB1C1=∠B2B3C3=α,且sinα=$\frac{4}{5}$,设BC=xm,B1B2=ym.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com