
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据新定义,对每个函数一一验证,即可得出结论.
解答 解:①f(x)=x3,|f(x)|=|x3|≤$\frac{k}{2016}$|x|,即|x2|≤$\frac{k}{2016}$,不存在这样的k对一切实数x均成立,
②f(x)=$\sqrt{3}$sinx+cosx=2sin(x+$\frac{π}{6}$),|f(x)|=|2sin(x+$\frac{π}{6}$)|≤$\frac{k}{2016}$|x|,
x=0时,|f(x)|=1≤0,不成立;
③f(x)=$\frac{x}{{x}^{2}+x+1}$,则|f(x)|=|$\frac{x}{{x}^{2}+x+1}$|=$\frac{|x|}{{(x+\frac{1}{2})}^{2}+\frac{3}{4}}$≤$\frac{4}{3}$|x|,
故对任意的$\frac{k}{2016}$>$\frac{4}{3}$,都有|f(x)|<$\frac{k}{2016}$|x|,故③正确;
④f(x)=$\frac{x}{{2}^{x}+1}$,|f(x)|=$\frac{|x|}{{2}^{x}+1}$≤$\frac{k}{2016}$|x|,故④正确;
故选:B.
点评 本题主要考查学生的阅读理解能力.知识点方面主要考查了函数的最值及其几何意义,综合性较强.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<1且x≠0} | B. | $\left\{x\right.|-1<x<-\frac{1}{2}$或$\frac{1}{2}<x<\left.1\right\}$ | ||
| C. | $\left\{{x|-\frac{1}{2}}\right.<x<\frac{1}{2}$且x≠0} | D. | {x|-1<x<-$\frac{1}{2}$或$0<x<\left.{\frac{1}{2}}\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
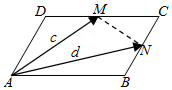 (1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知$\overrightarrow{AM}=\overrightarrow{c}$、$\overrightarrow{AN}=\overrightarrow{d}$,试用$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知$\overrightarrow{AM}=\overrightarrow{c}$、$\overrightarrow{AN}=\overrightarrow{d}$,试用$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com