
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 先判定函数f(x)的奇偶性与单调性,即可得出.
解答 解:∵$f(x)={x^5}+ln(x+\sqrt{{x^2}+1})$,x∈R.
∴f(-x)+f(x)=(-x)5+$ln(-x+\sqrt{{x}^{2}+1})$+x5+ln$(x+\sqrt{{x}^{2}+1})$=ln(-x2+x2+1)=0,
∴函数f(x)是R上的奇函数,
又函数f(x)在R上单调递增.
则对任意实数a,b,“a+b≥0”?a≥-b?f(a)≥f(-b)=-f(b)?“f(a)+f(b)≥0”.
∴对任意实数a,b,“a+b≥0”是“f(a)+f(b)≥0”的充要条件.
故选:C.
点评 本题考查了函数的奇偶性与单调性、不等式的性质,考查了推理能力与计算能力,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
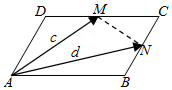 (1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知$\overrightarrow{AM}=\overrightarrow{c}$、$\overrightarrow{AN}=\overrightarrow{d}$,试用$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知$\overrightarrow{AM}=\overrightarrow{c}$、$\overrightarrow{AN}=\overrightarrow{d}$,试用$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x5 | B. | (x-1)5-1 | C. | x5+1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,1<f(x)<2 | B. | ?x0∈R,1<f(x0)<2 | ||
| C. | ?x∈R,f(x)≥2或f(x)≤1 | D. | ?x0∈R,f(x0)≥2或f(x0)>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{13}$ | C. | 5$\sqrt{2}$ | D. | $\sqrt{2}+2\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com