
分析 (1)求导,在x=2处取得极值,可得f′(2)=2+a+1=0,利用导数求单调区间;
(2)利用导数求出原函数的单调区间和极值,模拟函数图象;方程f(x)=m有三个实数x1,x2,x3(x1<x2<x3),等价于函数y=f(x)与直线y=m有三个交点,
根据函数图象得出x的范围.
解答 解:(1)f′(x)=x+a+$\frac{2}{x}$,
∵在x=2处取得极值,
∴f′(2)=2+a+1=0,
∴a=-3,
∴f′(x)=x-3+$\frac{2}{x}$=$\frac{(x-2)(x-1)}{x}$,
当x∈(0,1)和(2,+∞)时,f′(x)>0,f(x)递增,
当x∈(1,2)时,f′(x)<0,f(x)递减;
(2)由(1)可知:f(1)=$\frac{5}{2}$是函数f(x)的极大值;f(2)=ln4-4是函数f(x)的极小值,
∵方程f(x)=m有三个实数x1,x2,x3(x1<x2<x3);
∴函数y=f(x)与直线y=m有三个交点,
画出函数y=f(x)与y=m的图象,如图所示:
由图可知:ln4-4<m<$\frac{5}{2}$;则$\frac{1}{2}$<x1<1;2<x3<$\frac{5}{2}$
∴x3-x1<$\frac{5}{2}$-$\frac{1}{2}$=2.
点评 考察了极值点的概念,利用导函数求单调区间和极值并模拟函数图象,利用图象法证明问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | [-1,3) | C. | (1,2] | D. | [1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
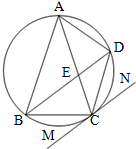 如图,四边形ABCD内接于圆,AB=AC,直线MN切圆于点C,BD∥MN交AC于点E.若AB=6,BC=4,则AE的长为$\frac{10}{3}$.
如图,四边形ABCD内接于圆,AB=AC,直线MN切圆于点C,BD∥MN交AC于点E.若AB=6,BC=4,则AE的长为$\frac{10}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
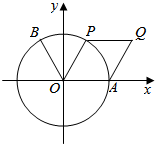 如图,点B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),点A时单位圆与x轴正半轴的交点.设点P为单位圆上的动点,点Q满足$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$,∠AOP=2θ($\frac{π}{6}$≤θ<$\frac{π}{2}$),f(θ)=$\overrightarrow{OB}$•$\overrightarrow{OQ}$,求f(θ)的取值范围,当$\overrightarrow{OB}$⊥$\overrightarrow{OQ}$时,求四边形OAQP的面积.
如图,点B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),点A时单位圆与x轴正半轴的交点.设点P为单位圆上的动点,点Q满足$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$,∠AOP=2θ($\frac{π}{6}$≤θ<$\frac{π}{2}$),f(θ)=$\overrightarrow{OB}$•$\overrightarrow{OQ}$,求f(θ)的取值范围,当$\overrightarrow{OB}$⊥$\overrightarrow{OQ}$时,求四边形OAQP的面积.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
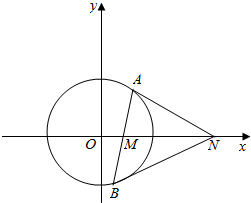 如图,已知圆O:x2+y2=r2(r>0),动直线l过点M(1,0)交圆O于A(x1,y1),B(x2,y2)两点(点A在x轴上方),点N在x轴上,若点B的坐标为(0,-r),则点A的横坐标为$\frac{8}{5}$.
如图,已知圆O:x2+y2=r2(r>0),动直线l过点M(1,0)交圆O于A(x1,y1),B(x2,y2)两点(点A在x轴上方),点N在x轴上,若点B的坐标为(0,-r),则点A的横坐标为$\frac{8}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com