
分析 (1)存在x∈R,使f(x)<b•g(x),即存在x∈R,x2-bx+b<0,则△>0,即b2-4b>0,
即可得到b的取值范围.
(2)由题意可知x2-mx+1≥0在区间[2,5]上恒成立,
即$m≤x+\frac{1}{x}$在区间[2,5]上恒成立,求出$y=x+\frac{1}{x}$得最小值即可,
解答 解:(1)存在x∈R,使f(x)<b•g(x),即存在x∈R,x2-bx+b<0,
则△>0,即b2-4b>0,
所以b的取值范围为(-∞,0)∪(4,+∞);
(2)由题意可知x2-mx+1≥0在区间[2,5]上恒成立,
即$m≤x+\frac{1}{x}$在区间[2,5]上恒成立,
由于$y=x+\frac{1}{x}$在[2,5]上单调递增,所以当x=2时,$y=x+\frac{1}{x}$有最小值$\frac{5}{2}$,
所以$m≤\frac{5}{2}$.即 实数m的取值范围为(-$∞,\frac{5}{2}$].
点评 本题考查了二次函数的性质,分离参数法求参数的范围,属于中档题.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
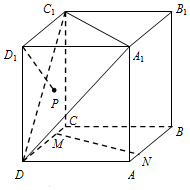 在正方体ABCD-A1B1C1D1中,点M、N分别是直线CD、AB上的动点,点P是△A1C1D内的动点(不包括边界),记直线D1P与MN所成角为θ,若θ的最小值为$\frac{π}{3}$,则点P的轨迹是( )
在正方体ABCD-A1B1C1D1中,点M、N分别是直线CD、AB上的动点,点P是△A1C1D内的动点(不包括边界),记直线D1P与MN所成角为θ,若θ的最小值为$\frac{π}{3}$,则点P的轨迹是( )| A. | 圆的一部分 | B. | 椭圆的一部分 | C. | 抛物线的一部分 | D. | 双曲线的一部分 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
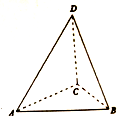 如图,在三棱锥D-ABC中,$AC=BC=1,CD=AB=\sqrt{2},AD=BD=\sqrt{3}$,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )
如图,在三棱锥D-ABC中,$AC=BC=1,CD=AB=\sqrt{2},AD=BD=\sqrt{3}$,若该三棱锥的四个顶点均在同一球面上,则该球的体积为( )| A. | $\frac{32π}{3}$ | B. | 4π | C. | 2π | D. | $\frac{4π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2ln2-2-(ln2)3 | B. | -1 | C. | 2ln2-2-(ln2)2k | D. | (k-1)ek-k3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,点O为正方体ABCD A′B′C′D′的中心,点E为棱B′B的中点,若AB=1,则下面说法正确的是( )
如图所示,点O为正方体ABCD A′B′C′D′的中心,点E为棱B′B的中点,若AB=1,则下面说法正确的是( )| A. | 直线AC与直线EC′所成角为45° | |
| B. | 点E到平面OCD′的距离为$\frac{1}{2}$ | |
| C. | 四面体O EA′B′在平面ABCD上的射影是面积为$\frac{1}{6}$的三角形 | |
| D. | 过点O,E,C的平面截正方体所得截面的面积为$\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) | [90,95) |
| 人数 | 1 | 3 | 6 | 6 | 2 | 1 | 1 |
| A. | 70分 | B. | 75分 | C. | 80分 | D. | 85分 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com