练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．如图所示算法，若输入的x的值为2017，则算法执行后的输出结果是（　　）
    A．2016B．2017C．2D．0

    分析 分析算法语句知程序运行后输出分段函数，计算x=2017时y的值即可．

    解答 解：分析该算法语句知，程序运行后输出
    y=$\left\{\begin{array}{l}{{（x+2015）}^{0}-1，x＞2016}\\{{（x-2015）}^{0}+1，x≤2016}\end{array}\right.$；
    当输入的x=2017时，算法执行后的输出结果是：
    y=（2017+2015）0-1=0．
    故选：D．

    点评 本题考查了根据流程图（或伪代码）写程序运行结果的问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．已知一组数据3、4、5、s、t的平均数是4，中位数是m，对于任意实数s、t，从3、4、5、s、t、m这组数据中任取一个，取到数字4的概率的最大值为（　　）
    A．$\frac{1}{6}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

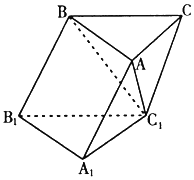    1．如图，在斜三棱柱中ABC-A1B1C1中，∠BAC=90°，BC1⊥AC，点P为AC1上的一个动点，则点P在底面ABC上的射影H必在（　　）
    A．直线AB上B．直线BC上C．直线AC上D．△ABC内部

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．如果执行如图的框图，则输出的数S=（　　）
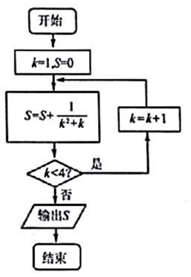
    A．$\frac{5}{4}$B．$\frac{4}{5}$C．$\frac{6}{5}$D．$\frac{5}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数$f（x）=2\sqrt{3}sinωxcosωx-2{cos^2}ωx+1（ω＞0）$，且y=f（x）的图象与直线y=2的两个相邻公共点之间的距离为π．
    （1）求函数f（x）的解析式，并求出f（x）的单调递增区间；
    （2）将函数f（x）的图象上所有点向左平移$\frac{π}{6}$个单位，得到函数g（x）的图象，设A，B，C为△ABC的三个内角，若g（B）-2=0，且向量$\overrightarrow m=（cosA，cosB）$，$\overrightarrow n=（1，sinA-cosAtanB）$，求$\overrightarrow m•\overrightarrow n$的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．过点P（4，3），且斜率为$\frac{2}{3}$的直线的参数方程为（　　）
    A．$\left\{\begin{array}{l}{x=4+\frac{3}{\sqrt{13}}t}\\{y=3+\frac{2}{\sqrt{13}}t}\end{array}\right.$（t为参数）B．$\left\{\begin{array}{l}{x=3+\frac{3}{\sqrt{13}}t}\\{y=4+\frac{2}{\sqrt{13}}t}\end{array}\right.$（t为参数）
    C．$\left\{\begin{array}{l}{x=4+\frac{2}{\sqrt{13}}t}\\{y=3+\frac{3}{\sqrt{13}}t}\end{array}\right.$（t为参数）D．$\left\{\begin{array}{l}{x=3+\frac{2}{\sqrt{13}}t}\\{y=4+\frac{3}{\sqrt{13}}t}\end{array}\right.$（t为参数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．如图是某学校某年级的三个班在一学期内的六次数学测试的平均成绩y关于测试序号x的函数图象，为了容易看出一个班级的成绩变化，将离散的点用虚线连接，根据图象，给出下列结论：
    ①一班成绩始终高于年级平均水平，整体成绩比较好；
    ②二班成绩不够稳定，波动程度较大；
    ③三班成绩虽然多数时间低于年级平均水平，但在稳步提升．
    其中正确结论的个数为（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知ξ的分布列为：
    ξ1234
    P$\frac{1}{4}$$\frac{1}{3}$$\frac{1}{6}$$\frac{1}{4}$
    则Eξ等于（　　）
    A．$\frac{29}{12}$B．$\frac{131}{144}$C．$\frac{11}{144}$D．$\frac{179}{144}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．命题p：|x-c|＜1，命题$q：\frac{4}{7-x}＞1$；若p是q的充分不必要条件，则实数c的取值范围为[4，6]．

    查看答案和解析>>

    同步练习册答案