
| 2 |
| a |
| AO |
| AB |
| AC |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
| AB |
| AC |
| AO |
| AB |
| AC |
|
| 2 |
| a |
| AB |
| AC |
| AO |
| AB |
| AC |
|
|
| 2 |
| 3 |
| 1 |
| 3a2 |
| 2 |
| 3 |
| a2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3a2 |
| a2 |
| 3 |
| 4 |
| 3 |
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 如图,焦距为2的椭圆E的两个顶点分别为A和B,且
如图,焦距为2的椭圆E的两个顶点分别为A和B,且| AB |
| n |
| 2 |
| OP |
| OQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知正三棱柱ABC-A1B1C的底面边长为4cm,高为7cm,则当一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的路程最短时,质点沿着侧面的前进方向所在直线与底面ABC所成角的余弦值为
已知正三棱柱ABC-A1B1C的底面边长为4cm,高为7cm,则当一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的路程最短时,质点沿着侧面的前进方向所在直线与底面ABC所成角的余弦值为查看答案和解析>>
科目:高中数学 来源: 题型:
 经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出15条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如图.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm.
经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出15条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如图.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm.查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
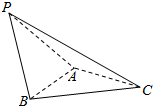 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com