
【题目】![]() 男
男![]() 女共
女共![]() 名同学从左至右排成一排合影,要求左端排男同学,右端排女同学,且女同学至多有
名同学从左至右排成一排合影,要求左端排男同学,右端排女同学,且女同学至多有![]() 人排在一起,则不同的排法种数为( )
人排在一起,则不同的排法种数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知2件次品和3件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结果.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的定义域为
的定义域为 ![]() ,若对于任意的
,若对于任意的 ![]() ,
, ![]() ,都有
,都有 ![]() ,且当
,且当 ![]() 时,有
时,有 ![]() .
.
(1)证明: ![]() 为奇函数;
为奇函数;
(2)判断 ![]() 在
在 ![]() 上的单调性,并证明;
上的单调性,并证明;
(3)设 ![]() ,若
,若 ![]() (
(![]() 且
且 ![]() )对
)对 ![]() 恒成立,求实数
恒成立,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.
A.[选修4-1:几何证明选讲]
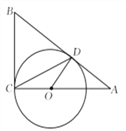
如图, ![]() 分别与圆
分别与圆![]() 相切于点
相切于点![]() ,
, ![]() ,
, ![]() 经过圆心
经过圆心![]() ,且
,且![]() ,求证:
,求证: ![]() .
.
B.[选修4-2:矩阵与变换]
在平面直角坐标系中,已知点![]() ,
, ![]() ,
, ![]() ,
, ![]() ,先将正方形
,先将正方形![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() ,再将所得图形的纵坐标压缩为原来的一半、横坐标不变,求连续两次变换所对应的矩阵
,再将所得图形的纵坐标压缩为原来的一半、横坐标不变,求连续两次变换所对应的矩阵![]() .
.
C.[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).现以
为参数).现以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,求曲线
轴的正半轴为极轴,建立极坐标系,求曲线![]() 的极坐标方程.
的极坐标方程.
D.[选修4-5:不等式选讲]
已知![]() 为互不相等的正实数,求证:
为互不相等的正实数,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
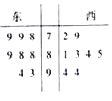
(1)根据茎叶图判断哪个区域厂家的平均分较高;
(2)规定85分以上(含85分)为优秀厂家,若从该两个区域各选一个优秀厂家,求得分差距不超过5分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两种坐标系中的长度单位相同,圆
轴的正半轴,两种坐标系中的长度单位相同,圆![]() 的直角坐标方程为
的直角坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),射线
为参数),射线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)已知射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
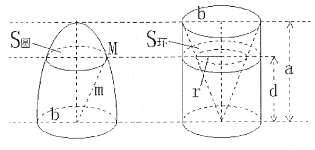
【题目】祖暅(公元前5-6世纪),祖冲之之子,是我国齐梁时代的数学家. 他提出了一条原理:“幂势既同,則积不容异. ”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等. 该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年. 椭球体是椭圆绕其轴旋转所成的旋转体. 如图将底面直径皆为![]() ,高皆为
,高皆为![]() 的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面
的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面![]() 上. 以平行于平面
上. 以平行于平面![]() 的平面于距平面
的平面于距平面![]() 任意高
任意高![]() 处可横截得到
处可横截得到![]() 及
及![]() 两截面,可以证明
两截面,可以证明![]() 知总成立. 据此,短轴长为
知总成立. 据此,短轴长为![]() ,长轴为
,长轴为![]() 的椭球体的体积是 __________
的椭球体的体积是 __________![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() ,定点
,定点![]() (常数
(常数![]() )的直线
)的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)若点![]() 的坐标为
的坐标为![]() ,求证:
,求证: ![]()
(2)若![]() ,以
,以![]() 为直径的圆的位置是否恒过一定点?若存在,求出这个定点,若不存在,请说明理由.
为直径的圆的位置是否恒过一定点?若存在,求出这个定点,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com