Question

4．已知直三棱柱ABC-A′B′C中，底面是以AC为斜边的等腰直角三角形，且AA′=AB，求异面直线AB′与BC′所成角．

Answer 1

分析 以B为原点，BA为x轴，BC为y轴，BB′为z轴，建立空间直角坐标系，利用向量法能求出异面直线AB′与BC′所成角．′

解答 以B为原点，BA为x轴，BC为y轴，BB′为z轴，建立空间直角坐标系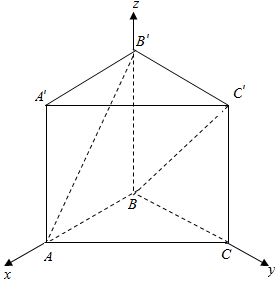
设AA₁=AB=1，AA′=t，
则A（1，0，0），B′（0，0，t），B（0，0，0），C′（0，1，0），
$\overrightarrow{A{B}^{'}}$=（-1，0，t），$\overrightarrow{B{C}^{'}}$=（0，1，0），
设异面直线AB′与BC′所成角为θ．
cosθ=$\frac{|\overrightarrow{A{B}^{'}}•\overrightarrow{B{C}^{'}}|}{|\overrightarrow{A{B}^{'}}|•|\overrightarrow{B{C}^{'}}|}$=0，⑥
∴θ=90°，
∴异面直线AB′与BC′所成角为90°．

点评 本题考查异面直线所成角的求法，是基础题，解题时要认真审题，注意向量法的合理运用．