Question

8．设变量x，y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{y≥3x-6}\\{x+y≥2}\end{array}\right.$，则目标函数z=$lo{g}_{\sqrt{3}}$（2x+y）的最小值（　　）

• A． -2
• B． -1
• C． 1
• D． 2

Answer 1

分析 画出平面区域，利用目标函数的几何意义求最小值．

解答 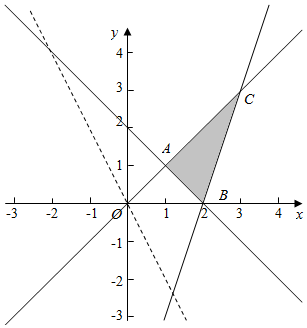解：已知约束条件对应的区域如图设z=2x+y，平移此直线，当过图中A时使得Z最小，由$\left\{\begin{array}{l}{y=x}\\{x+y=2}\end{array}\right.$得到A（1，1），
所以z的最小值为2+1=3，所以目标函数z=$lo{g}_{\sqrt{3}}$（2x+y）的最小值为$lo{g}_{\sqrt{3}}3=\frac{lg（\sqrt{3}）^{2}}{lg\sqrt{3}}$=2；
故选：D．

点评 本题考查了简单线性规划问题，利用了数形结合的思想解答；关键是正确画出平面区域，利用目标函数的几何意义求最值．