
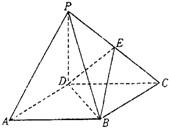
 如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.分析 (1)连结AC,设AC与BD交于O点,连结EO,易证EO为△PAC的中位线,从而OE∥PA,再利用线面平行的判断定理即可证得PA∥平面BDE;
(2)依题意,易证DE⊥底面PBC,再利用面面垂直的判断定理即可证得平面BDE⊥平面PBC;
(3)将几何体放到正方体中,则可得直线AB与平面PBC所成角的大小.
解答 (1)证明:连结AC,设AC与BD交于O点,连结EO,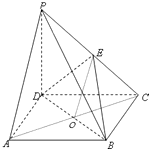
由O,E分别为AC,CP中点,
∴OE∥PA
又OE?平面EDB,PA?平面EDB,
∴PA∥平面EDB.(5分)
(2)证明:由PD⊥平面ABCD∴PD⊥BC又CD⊥BC,
∴BC⊥平面PCD,DE⊥BC.(8分)
由PD=DC,E为P中点,故DE⊥PC.
∴DE⊥平面PBC(10分)
(3)解:将几何体放到正方体中,则可得直线AB与平面PBC所成角的大小为45°.(14分)
点评 本题主要考查线与线,线与面,面与面的位置关系和线面平行和线面垂直的判定定理的灵活运用,培养学生形成知识网络及知识间相互转化的能力.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{100}$+$\frac{y^2}{36}$=1 | B. | $\frac{y^2}{400}$+$\frac{x^2}{336}$=1 | C. | $\frac{y^2}{100}$+$\frac{x^2}{36}$=1 | D. | $\frac{y^2}{20}$+$\frac{x^2}{12}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5$\sqrt{3}$N | B. | 5N | C. | 10N | D. | 5$\sqrt{2}$N |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com