
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 (1)将一组数据中的每个数据都减去同一个数后,平均数发生变化,标准差均没有变化,可判断(1);
(2)在线性回归分析中,相关系数r→-1,表明两个变量负相关越强,可判断(2);
(3)利用分层抽样的概念及运算公式可求得样本容量为n的值,从而可判断(3).
解答 解:(1)将一组数据中的每个数据都减去同一个数a后,平均数为原平均数减去a,其标准差没有变化,故(1)错误;
(2)在线性回归分析中,相关系数r接近-1,表明两个变量负相关越强,故(2)错误;
(3)某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本,若样本中的青年职工为7人,设样本容量为n,则$\frac{7}{n}$=$\frac{350}{350+250+150}$,解得n=15,故(3)正确.
故正确结论的个数为1个,
故选:B.
点评 本题考查概率统计中的均值与方差、回归分析中的相关系数的概念及应用、分层抽样及线面垂直的定义,属于中档题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | [2,e) | C. | $({e+\frac{1}{e},+∞})$ | D. | $[{2,e+\frac{1}{e}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | ln2 | C. | $\frac{π}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
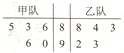 某项比赛规则是:先进行个人赛,每支参赛队的成绩前三名队员再代表本队进行团体赛,团体赛是在两队名次相同队员之间进行且三场比赛同时进行.根据以往比赛统计:两名队员中个人赛成绩高的队员在各场获胜的概率为$\frac{2}{3}$,负的概率为$\frac{1}{3}$,且各场比赛互不影响.已知甲乙队各5名队员,这10名队员的个人赛成绩如图所示:
某项比赛规则是:先进行个人赛,每支参赛队的成绩前三名队员再代表本队进行团体赛,团体赛是在两队名次相同队员之间进行且三场比赛同时进行.根据以往比赛统计:两名队员中个人赛成绩高的队员在各场获胜的概率为$\frac{2}{3}$,负的概率为$\frac{1}{3}$,且各场比赛互不影响.已知甲乙队各5名队员,这10名队员的个人赛成绩如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com