
���� ������ֱ�߷������F2��b��0����c=b����a=$\sqrt{2}$c�����������Բ�ı����̣�
����1�����õ㵽ֱ�ߵľ��빫ʽ��������Բ���̣����P�����꣬���������ε������ʽ�������b��ֵ�����������Բ���̣�
��2���������ۣ���ֱ��б��k��0ʱ��������Բ���̣��ɡ�-0�����m��k�Ĺ�ϵ����ã�|F1M|+|F2N|��•|MNح�����û�������ʽ�����ʼ�����ã�|F1M|+|F2N|��•|MNحȡֵ��Χ����k=0���ı���F1MF2NΪ���Σ���|F1M|+|F2N|��•|MN|=��1+1����2=4��������ã�|F1M|+|F2N|��•|MN|�����ֵ��
��� �⣺������ֱ��BF2�ķ���Ϊx-y-b=0����F2��b��0����c=b��
��a2=b2+c2=2c2��
��Բ��������e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$��
����ԲC��������$\frac{\sqrt{2}}{2}$��
����1����P��x0��y0������$\frac{ح{x}_{0}-{y}_{0}-bح}{\sqrt{2}}$=$\sqrt{2}$b��
��x0-y0-3b=0����x0-y0+b=0��
��$\left\{\begin{array}{l}{x-y-3b=0}\\{{x}^{2}+2{y}^{2}=2{b}^{2}}\end{array}\right.$���⣬
$\left\{\begin{array}{l}{x-y+b=0}\\{{x}^{2}+2{y}^{2}=2{b}^{2}}\end{array}\right.$����ã�$\left\{\begin{array}{l}{x=-\frac{4}{3}b}\\{y=-\frac{1}{3}b}\end{array}\right.$��
�ɡ�PF1F2�����ΪS=$\frac{1}{2}$��2b��$\frac{1}{3}$b=$\frac{1}{3}$��
��ã�b=1��
����Բ�ı�����Ϊ��$\frac{{x}^{2}}{2}+{y}^{2}=1$��
��2����ֱ��l��y=kx+m��
��$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$���������2k2+1��x2+4kmx+2m2-2=0��
�ɡ�=��4km��2-4��2k2+1����2m2-2��=0��������m2=2k2+1��
حF1Mح=$\frac{حm-kح}{\sqrt{1+{k}^{2}}}$��حF2Mح=$\frac{حm+kح}{\sqrt{1+{k}^{2}}}$��
��k��0ʱ����حMNح=$\frac{ح{F}_{1}Mح-ح{F}_{2}Nح}{k}$��
��|F1M|+|F2N|��•|MN|=$\frac{4حkmح}{��1+{k}^{2}��حkح}$=$\frac{4حmح}{��1+{k}^{2}��}$=$\frac{4حmح}{1+\frac{{m}^{2}-1}{2}}$=$\frac{8}{حmح+\frac{1}{حmح}}$��4��
���ҽ���حmح=1ʱ��ȡ�Ⱥţ�
��k��0����حmح��1����ˣ�|F1M|+|F2N|��•|MN|��4��
��k=0ʱ���ı���F1MF2NΪ���Σ�
��ʱ��|F1M|+|F2N|��•|MN|=��1+1����2=4��
���Ͽ�֪����|F1M|+|F2N|��•|MN|�����ֵΪ4��
���� ���⿼����Բ�ı����̼��������ʣ�ֱ������Բ��λ�ù�ϵ��������Բ���������ʽ���ۺ����ã������������˼�룬�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
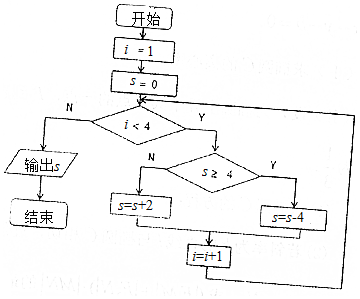
| A�� | 0 | B�� | 2 | C�� | 4 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{3}$ | B�� | $-\frac{2}{3}$ | C�� | $\frac{3}{2}$ | D�� | $-\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com