
分析 先根据题意画出图形,再设三棱柱外接球的球半径为r,利用在直角三角形ADO中的边的关系求出正三棱本的高,作出空间直角坐标系,利用向量法能求出异面直线AB1与BC1所成角的余弦值.
解答 解:设三棱柱外接球的球心为O,球半径为r,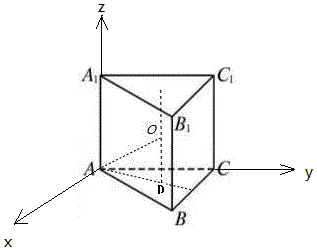
三棱柱的底面三角形ABC的中心为D,如图,
∵正三棱柱ABC-A1B1C1底面△ABC的边长为3,此三棱柱的外接球的半径为$\sqrt{7}$,
∴OA=$\sqrt{7}$,AD=$\frac{2}{3}×\sqrt{{3}^{2}-(\frac{3}{2})^{2}}$=$\sqrt{3}$,
∴OD=$\sqrt{7-3}$=2,∴AA1=4,
以A为原点,以过A在平面ABC中作AC的垂线为x轴,以AC为y轴,AA1为z轴,
建立空间直角坐标系,
A(0,0,0),B($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$,0),
B1($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$,4),C1(0,3,4),
$\overrightarrow{A{B}_{1}}$=($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$,4),$\overrightarrow{B{C}_{1}}$=(-$\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$,4),
设异面直线AB1与BC1所成角为θ,
则cosθ=$\frac{|\overrightarrow{A{B}_{1}}•\overrightarrow{B{C}_{1}}|}{|\overrightarrow{A{B}_{1}}|•|\overrightarrow{B{C}_{1}}|}$=$\frac{\frac{23}{2}}{25}$=$\frac{23}{50}$.
∴异面直线AB1与BC1所成角的余弦值为$\frac{23}{50}$.
故答案为:$\frac{23}{50}$.
点评 本题考查三棱锥、球、空间中线线、线面间的相互关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,考查创新意识、应用意识,是中档题.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{\sqrt{2}+1}{2}$ | C. | $\frac{3+2\sqrt{2}}{2}$ | D. | $\frac{\sqrt{5}+1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
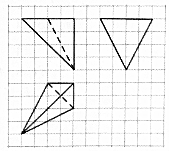 如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的体积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的体积为( )| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{32}{3}$ | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | π | C. | 4π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
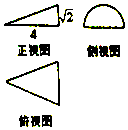 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )| A. | $\frac{4}{3}$π | B. | $\frac{4\sqrt{2}}{3}$π | C. | 4π | D. | 4$\sqrt{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com