练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知数列{an}是等差数列，若a3+a11=24，a4=3，则数列{an}的公差=3．

    分析 根据等差数列的通项公式，列出方程，解方程即可求出数列的公差．

    解答 解：数列{an}是等差数列，若a3+a11=24，a4=3，
    则（a4-d）+（a4+7d）=（3-d）+（3+7d）=24，
    解得d=3，
    所以数列{an}的公差为3．
    故答案为：3．

    点评 本题考查了等差数列的通项公式与应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．与不等式（x+3）（x-5）＜0的解集相同的是（　　）
    A．$\left\{\begin{array}{l}x+3＞0\\ x-5＜0\end{array}\right.$B．$\left\{\begin{array}{l}x+3＜0\\ x-5＞0\end{array}\right.$C．$\left\{\begin{array}{l}x-5＞0\\ x+3＜0\end{array}\right.$D．$\left\{\begin{array}{l}x+3＞0\\ x-5＞0\end{array}\right.$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知{an}为等差数列，且a4+a7+a10=30，则a1-a3-a6-a8-a11+a13的值为（　　）
    A．10B．-10C．20D．-20

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．化简：$\frac{{C_m^m+2C_{m+1}^m+3C_{m+2}^m+…+nC_{m+n-1}^m}}{{C_{m+n}^{m+1}}}$=$\frac{（m+1）n+1}{m+2}$（用m、n表示）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知命题p：?x∈R，x2+2x+m≤0，命题q：指数函数f（x）=（3-m）x是增函数，若“p∨q”为真命题，“p∧q”为假命题，则实数m的取值范围是（1，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

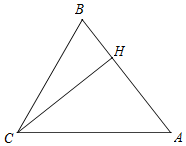    19．已知三角形△ABC中，∠ACB=60°，CH为AB边上的高，H为垂足；设BC=a，CA=b，AB=c，CH=h；
    （1）若c=$\sqrt{3}$，求a+b的取值范围；
    （2）若已知h=$\sqrt{3}$，试解决下面两个问题：
    ①求a，b满足的等式；
    ②求三角形ABC的周长l的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知多项式f（x）=x6+3x5-2x4+5x2+x-2，利用秦九韶算法计算当x=3时，v3=48．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．若函数f（x）=log2[（a+2）x2+（a+2）x+1]的定义域为R，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．从某工厂生产的某产品中抽取500件，测量这些产品的一项质量指标，由测量结果得到下列频数分布表：
    指标值分组[75，85）[85，95）[95，105）[105，115）[115，125]
    频数3012021010040
    （1）作出这些数据的频率分布直方图，并估计该产品质量指标值的平均数$\overline x$及方差s2（同一组中的数据用该组的中点值作代表）；
    （2）可以认为这种产品的质量指标值Z服从正态分布N（μ，σ2），其中μ近似为样本平均数$\overline x$，σ2．近似为样本方差s2； 一件产品的质量指标不小于110时该产品为优质品；利用该正态分布，计算这种产品的优质品率p（结果保留小数点后4位）．
    （以下数据可供使用：若Z～N（μ，δ2），则P（μ-δ＜ξ＜μ+δ）=68.26%，P（μ-2δ＜ξ＜μ+2δ）=95.44%）

    查看答案和解析>>

    同步练习册答案