练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知ω>0，函数f(x)＝cos(ωx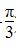＋)的一条对称轴为x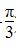＝，一个对称中心为点(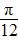，0)，则ω有(　　)

    A．最小值2                                                  B．最大值2

    C．最小值1                                                  D．最大值1


    A

    [解析]　由题意知－≥，∴T＝≤π，∴ω≥2，故选A.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某商人将进货单价为8元的某种商品按10元一个销售时，每天可卖出100个，现在他采用提高售价，减少进货量的办法增加利润，已知这种商品销售单价每涨1元，销售量就减少10个，问他将售价每个定为多少元时，才能使每天所赚的利润最大？并求出最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知角α是第n(n＝1、2、3、4)象限的角，问是第几象限的角？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知tanθ>1，且sinθ＋cosθ<0，则cosθ的取值范围是(　　)

    A．(－，0)                                             B．(－1，－)

    C．(0，)                                                D．(，1)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    sin45°cos15°＋cos225°sin15°的值为(　　)

    A．－                                                     B．－

    C.                                                             D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)＝(1＋tanx)cosx,0≤x<，则f(x)的最大值为(　　)

    A．1                                                             B．2

    C.＋1                                                      D.＋2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知m＝(asinx，cosx)，n＝(sinx，bsinx)，其中a，b，x∈R.若f(x)＝m·n满足f(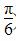)＝2，且f(x)的导函数f ′(x)的图象关于直线x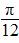＝对称．

    (1)求a，b的值；

    (2)若关于x的方程f(x)＋log2k＝0在区间[0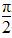，]上总有实数解，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝cos2ax－sin2ax的最小正周期为π，则a的值是(　　)

    A．－1                                                          B．1

    C．2                                                             D．±1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面几何里，有勾股定理：“设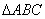的两边AB、AC互相垂直，则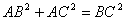。”拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面积与底面积间的关系，可以得到的正确结论是：“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直，则                             ”。

    查看答案和解析>>

    同步练习册答案