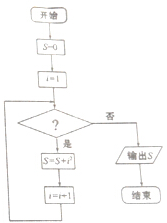
考点:向量在几何中的应用
专题:平面向量及应用
分析:取AC中点为D,则OD⊥AC,把写为
=
+
,然后用两种方法写出,由数量积相等结合2x+10y=5,需要分类讨论,当x≠0求得cos∠BAC,进一步得到其正弦值,代入三角形的面积公式求得三角形ABC的面积,当x=0时,得到三角形为直角三角形,求出面积,问题得以解决
解答:
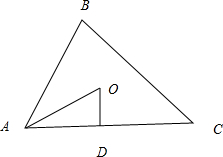
解:取AC的中点,则OD⊥AC,
⊥
如图所示∵
=
+
,
∴
•
=
•
+
•=
||•||COS0=5×10=50,
∵
=x
+y
,
∴
•
=(x
+y
)•
=x
•+y
||2=x|
||
|cos∠BAC+y
||2=60x•cos∠BAC+100y,
∴60x•cos∠BAC+100y=50
∵2x+10y=5,
∴60xcos∠BAC=20x,
当x≠0时,
∴cos∠BAC=
,
∴sin∠BAC=
,
∴S
△ABC=
AB•AC•sin∠BAC=
×6×10×
=20
当x=0时,则y=
,
∴
=0
+
,
∴
=
,
∴点A,0,C共线,
∴即点O为AC的中点,
∴三角形ABC以B为直角的直角三角形,
∴BC=
=
=8,
∴S
△ABC=
AB•BC=
×6×8=24
故选:D
点评:本题考查了向量在几何中的应用,考查了平面向量的数量积运算,考查了三角形面积公式的应用,是中档题.

 解:取AC的中点,则OD⊥AC,
解:取AC的中点,则OD⊥AC,

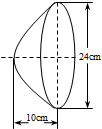 如图所示,汽车前灯反光镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反光镜的轴垂直,灯泡位于抛物线的焦点处.已知灯口的直径是24cm,灯深10cm,那么灯泡与反光镜的顶点(即截得抛物线的顶点)距离为( )
如图所示,汽车前灯反光镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反光镜的轴垂直,灯泡位于抛物线的焦点处.已知灯口的直径是24cm,灯深10cm,那么灯泡与反光镜的顶点(即截得抛物线的顶点)距离为( )