Question

4．已知矩形ABCD中，AB=4$\sqrt{3}$，BC=4，M，N分别是边BC，CD上的点，且MN=2，则$\overrightarrow{AM}•\overrightarrow{AN}$的最小值是（　　）

• A． 12
• B． 24
• C． 36
• D． 48

Answer 1

分析 由题意画出图形，建立适当的平面直角坐标系，设出M，N的坐标，结合MN=2，得$（c-4\sqrt{3}）^{2}+（b-4）^{2}=4$，令c=$4\sqrt{3}+2cosα$，b=4+2sinα，把$\overrightarrow{AM}•\overrightarrow{AN}$转化为含有α的三角函数求得最值．

解答 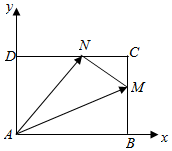解：如图，分别以AB，AD所在直线为x，y轴建立平面直角坐标系，
则A（0，0），B（$4\sqrt{3}$，0），D（0，4），C（$4\sqrt{3}，4$），
设M（$4\sqrt{3}，b$），N（c，4），
则$\overrightarrow{MN}=（c-4\sqrt{3}，4-b）$，
由MN=2，得$（c-4\sqrt{3}）^{2}+（b-4）^{2}=4$，
令c=$4\sqrt{3}+2cosα$，b=4+2sinα，
则$\overrightarrow{AM}•\overrightarrow{AN}$=$4\sqrt{3}c+4b=48+8\sqrt{3}cosα+16+8sinα$
=$64+16sin（α+\frac{π}{3}）$．
∴当sin（$α+\frac{π}{3}$）取最小值-1时，$\overrightarrow{AM}•\overrightarrow{AN}$有最小值是48．
故选：D．

点评 本题考查平面向量的数量积运算，考查数学转化思想方法，训练了三角函数最值的求法，是中档题．