
【题目】数列{an}的前n项a1 , a2 , …,an(n∈N*)组成集合An={a1 , a2 , …,an},从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),例如:对于数列{2n﹣1},当n=1时,A1={1},T1=1;n=2时,A2={1,3},T1=1+3,T2=13;
(1)若集合An={1,3,5,…,2n﹣1},求当n=3时,T1 , T2 , T3的值;
(2)若集合An={1,3,7,…,2n﹣1},证明:n=k时集合Ak的Tm与n=k+1时集合Ak+1的Tm(为了以示区别,用Tm′表示)有关系式Tm′=(2k+1﹣1)Tm﹣1+Tm , 其中m,k∈N*,2≤m≤k;
(3)对于(2)中集合An . 定义Sn=T1+T2+…+Tn , 求Sn(用n表示).
【答案】
(1)解:当n=3时,A3={1,3,7},
T1=1+3+7=11,T2=1×3+1×7+3×7=31,T3=1×3×7=21
(2)证明:当n=k+1时,集合Ak+1有k+1个元素,比n=k时的集合Ak多了一个元素:ak+1=2k+1﹣1.∴对应的 ![]() 包含两个部分:(i)若
包含两个部分:(i)若 ![]() 中不含ak+1,则
中不含ak+1,则 ![]() 中的任何一项恰好为n=k时集合Ak的对应的Tm中的一项.
中的任何一项恰好为n=k时集合Ak的对应的Tm中的一项.
(ii)若 ![]() 中含ak+1的任何一项,除了ak+1,其余的m﹣1个数均来自集合Ak,这m﹣1个数的乘积恰好为集合Ak所对应的Tm﹣1中的一项.
中含ak+1的任何一项,除了ak+1,其余的m﹣1个数均来自集合Ak,这m﹣1个数的乘积恰好为集合Ak所对应的Tm﹣1中的一项.
∴有关系式Tm′=(2k+1﹣1)Tm﹣1+Tm,其中m,k∈N*,2≤m≤k
(3)解:由S1=1=21﹣1=1,S2=7=23﹣1,S3=63=26﹣1,
猜想 Sn= ![]() ﹣1.下面证明:
﹣1.下面证明:
(i)易知n=1时成立.
(ii)假设n=k时,Sn=Sk= ![]() ﹣1,
﹣1,
则n=k+1时,Sk+1=T1+T2+T3+…+Tk+1
=[T1′+(2k+1﹣1)]+[T2′+(2k+1﹣1)T1′]+[T3′+(2k+1﹣1)T2′]+…+[Tk′+(2k+1﹣1)]
(其中Ti′,i=1,2,…,k,为n=k时可能的k个数的乘积的和为Tk),
=( T1′+T2′+T3′+…+Tk′)+(2k+1﹣1)+(2k+1﹣1)( T1′+T2′+T3′+…+Tk′)
=Sk+(2k+1﹣1)+(2k+1﹣1)Sk = ![]() +(2k+1﹣1)
+(2k+1﹣1)
= ![]() ﹣1,
﹣1,
即n=k+1时,Sk+1═ ![]() ﹣1也成立,
﹣1也成立,
综合(i)(ii)知对n∈N*,Sn= ![]() ﹣1成立.
﹣1成立.
∴Sn= ![]() ﹣1
﹣1
【解析】(1)当n=3时,A3={1,3,7},由定义可得:T1 , T2 , T3的值.(2)当n=k+1时,集合Ak+1有k+1个元素,比n=k时的集合Ak多了一个元素:ak+1=2k+1﹣1.对应的 ![]() 包含两个部分:(i)若
包含两个部分:(i)若 ![]() 中不含ak+1 , 则
中不含ak+1 , 则 ![]() 中的任何一项恰好为n=k时集合Ak的对应的Tm中的一项.(ii)若
中的任何一项恰好为n=k时集合Ak的对应的Tm中的一项.(ii)若 ![]() 中含ak+1的任何一项,除了ak+1 , 其余的m﹣1个数均来自集合Ak , 这m﹣1个数的乘积恰好为集合Ak所对应的Tm﹣1中的一项.即可证明.(3)由S1=1=21﹣1=1,S2=7=23﹣1,S3=63=26﹣1,猜想 Sn=
中含ak+1的任何一项,除了ak+1 , 其余的m﹣1个数均来自集合Ak , 这m﹣1个数的乘积恰好为集合Ak所对应的Tm﹣1中的一项.即可证明.(3)由S1=1=21﹣1=1,S2=7=23﹣1,S3=63=26﹣1,猜想 Sn= ![]() ﹣1.下面利用数学归纳法证明即可.
﹣1.下面利用数学归纳法证明即可.
【考点精析】通过灵活运用数列的前n项和,掌握数列{an}的前n项和sn与通项an的关系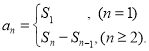 即可以解答此题.
即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】奇函数f(x)定义域为(﹣π,0)∪(0,π),其导函数是f′(x).当0<x<π时,有f′(x)sinx﹣f(x)cosx<0,则关于x的不等式f(x)< ![]() f(
f( ![]() )sinx的解集为( )
)sinx的解集为( )
A.( ![]() ,π)
,π)
B.(﹣π,﹣ ![]() )∪(
)∪( ![]() ,π)
,π)
C.(﹣ ![]() ,0)∪(0,
,0)∪(0, ![]() )
)
D.(﹣ ![]() ,0)∪(
,0)∪( ![]() ,π)
,π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某商品每吨的价格为x(1<x<14)万元时,该商品的月供给量为y1吨,y1=ax+ ![]() a2﹣a(a>0):月需求量为y2吨,y2=﹣
a2﹣a(a>0):月需求量为y2吨,y2=﹣ ![]() x2﹣
x2﹣ ![]() x+1,当该商品的需求量大于供给量时,销售量等于供给量:当该商品的需求量不大于供给量时,销售量等于需求量,该商品的月销售额等于月销售量与价格的乘积.
x+1,当该商品的需求量大于供给量时,销售量等于供给量:当该商品的需求量不大于供给量时,销售量等于需求量,该商品的月销售额等于月销售量与价格的乘积.
(1)已知a= ![]() ,若某月该商品的价格为x=7,求商品在该月的销售额(精确到1元);
,若某月该商品的价格为x=7,求商品在该月的销售额(精确到1元);
(2)记需求量与供给量相等时的价格为均衡价格,若该商品的均衡价格不低于每吨6万元,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={(x,y)|y=x2+2bx+1},B={(x,y)|y=2a(x+b)},且A∩B是单元素集合,若存在a<0,b<0使点P∈{(x,y)|(x﹣a)2+(y﹣b)2≤1},则点P所在的区域的面积为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f'(x)是函数f(x)的导数,f'(x)是函数f'(x)的导数,若方程f'(x)=0有实数解x0 , 则称点(x0 , f(x0))为函数f(x)的拐点.某同学经过探究发现:任何一个三次函数f(x)=ax3+bx2+cx+d(a≠0)都有拐点,任何一个三次函数都有对称中心,且拐点就是对称中心,
设函数g(x)=x3﹣3x2+4x+2,利用上述探究结果
计算: ![]() =
=
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a是常数,对任意实数x,不等式|x+1|﹣|2﹣x|≤a≤|x+1|+|2﹣x|都成立.
(Ⅰ)求a的值;
(Ⅱ)设m>n>0,求证:2m+ ![]() ≥2n+a.
≥2n+a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求f(x)单调递减区间;
(2)已知△ABC中,满足sin2B+sin2C>sinBsinC+sin2A,求f(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() 过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A,B两点.设点P(4,3),记PA,PB的斜率分别为k1和k2 .
过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A,B两点.设点P(4,3),记PA,PB的斜率分别为k1和k2 . 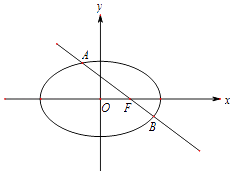
(1)求椭圆C的方程;
(2)如果直线l的斜率等于﹣1,求出k1k2的值;
(3)探讨k1+k2是否为定值?如果是,求出该定值;如果不是,求出k1+k2的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com