
【题目】已知a是常数,对任意实数x,不等式|x+1|﹣|2﹣x|≤a≤|x+1|+|2﹣x|都成立.
(Ⅰ)求a的值;
(Ⅱ)设m>n>0,求证:2m+ ![]() ≥2n+a.
≥2n+a.
【答案】(Ⅰ)解:|x+1|﹣|2﹣x|≤|x+1+2﹣x|=3,3=|x+1+2﹣x|≤|x+1|+|2﹣x|
∵对任意实数x,不等式|x+1|﹣|2﹣x|≤a≤|x+1|+|2﹣x|都成立,
∴a=3;
(Ⅱ)证明:2m+ ![]() ﹣2n=(m﹣n)+(m﹣n)+
﹣2n=(m﹣n)+(m﹣n)+ ![]() ,
,
∵m>n>0,
∴(m﹣n)+(m﹣n)+ ![]() ≥3
≥3 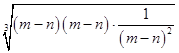 =3,
=3,
∴2m+ ![]() ﹣2n≥3,
﹣2n≥3,
即2m+ ![]() ≥2n+a
≥2n+a
【解析】(Ⅰ)利用绝对值不等式求最值,即可求a的值;
(Ⅱ)作差,利用基本不等式证明结论.
【考点精析】本题主要考查了绝对值不等式的解法和不等式的证明的相关知识点,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号;不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等才能正确解答此题.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】数列{an}的前n项a1 , a2 , …,an(n∈N*)组成集合An={a1 , a2 , …,an},从集合An中任取k(k=1,2,3,…,n)个数,其所有可能的k个数的乘积的和为Tk(若只取一个数,规定乘积为此数本身),例如:对于数列{2n﹣1},当n=1时,A1={1},T1=1;n=2时,A2={1,3},T1=1+3,T2=13;
(1)若集合An={1,3,5,…,2n﹣1},求当n=3时,T1 , T2 , T3的值;
(2)若集合An={1,3,7,…,2n﹣1},证明:n=k时集合Ak的Tm与n=k+1时集合Ak+1的Tm(为了以示区别,用Tm′表示)有关系式Tm′=(2k+1﹣1)Tm﹣1+Tm , 其中m,k∈N*,2≤m≤k;
(3)对于(2)中集合An . 定义Sn=T1+T2+…+Tn , 求Sn(用n表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差为2的等差数列,数列{bn}满足 ![]() ,若n∈N*时,anbn+1﹣bn+1=nbn .
,若n∈N*时,anbn+1﹣bn+1=nbn .
(Ⅰ)求{bn}的通项公式;
(Ⅱ)设cn=anbn , 求{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果一个数列从第2项起,每一项与它前一项的差都大于2,则称这个数列为“H型数列”.
(1)若数列{an}为“H型数列”,且a1= ![]() ﹣3,a2=
﹣3,a2= ![]() ,a3=4,求实数m的取值范围;
,a3=4,求实数m的取值范围;
(2)是否存在首项为1的等差数列{an}为“H型数列”,且其前n项和Sn满足Sn<n2+n(n∈N*)?若存在,请求出{an}的通项公式;若不存在,请说明理由.
(3)已知等比数列{an}的每一项均为正整数,且{an}为“H型数列”,bn= ![]() an , cn=
an , cn= ![]() ,当数列{bn}不是“H型数列”时,试判断数列{cn}是否为“H型数列”,并说明理由.
,当数列{bn}不是“H型数列”时,试判断数列{cn}是否为“H型数列”,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com