
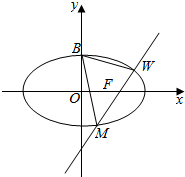
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,上顶点为B(0,1).
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,上顶点为B(0,1).分析 (Ⅰ)椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,上顶点为B(0,1),求出a,b,可得椭圆的方程;
(II)利用点差法,求出AB的斜率,可得直线AB的方程,代入椭圆方程,即可求线段AB的长.
(III)假设存在直线l与此椭圆交于M,W两点,使得△BMW的垂心为椭圆的右焦点F.设M(x1,y1),N(x2,y2),由B(0,1),F(1,0),kBF=-1.由BF⊥MN,知kMN=1.设直线l的方程为y=x+m,与椭圆的方程联立可得△>0即根与系数的关系,再利用$\overrightarrow{BM}$•$\overrightarrow{FN}$=0即可得出.
解答 解:(Ⅰ)∵椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,上顶点为B(0,1).
∴$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,b=1.
又a2-c2=b2,从而a=$\sqrt{2}$,c=1.
∴椭圆C的方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1.
(Ⅱ)设M(x1,y1),N(x2,y2),则
x12+2y12=2,x22+2y22=2,
两式相减可得(x1+x2)(x1-x2)+2(y1+y2)(y1-y2)=0,
∵线段MW的中点为(1,$\frac{1}{2}$),∴2(x1-x2)+2(y1-y2)=0,
∴直线MN的斜率为-1,
∴直线MN的方程为y-$\frac{1}{2}$=-(x-1),即2x+2y-3=0,
与椭圆方程联立可得3x2-6x-2.5=0,
∴|MN|=$\sqrt{1+1}$•$\sqrt{4+4×\frac{2.5}{3}}$=$\frac{2\sqrt{11}}{3}$.
(Ⅲ)假设存在直线l与此椭圆交于M,W两点,使得△BMW的垂心为椭圆的右焦点F.
∵B(0,1),F(1,0),∴kBF=-1.
由BF⊥MN,知kMN=1.
设直线l的方程为y=x+m,
代入$\frac{{x}^{2}}{2}+{y}^{2}$=1得3x2+4mx+2m2-2=0.
由△>0,得m2<3,且x1+x2=-$\frac{4m}{3}$,x1x2=$\frac{2{m}^{2}-2}{3}$.
由题意,有$\overrightarrow{BM}$•$\overrightarrow{FN}$=0.
∴x1(x2-1)+y2(y1-1)=0,即x1(x2-1)+(x2+m)(x1+m-1)=0,
∴2x1x2+(x1+x2)(m-1)+m2-m=0.
于是2•$\frac{2{m}^{2}-2}{3}$2+(-$\frac{4m}{3}$)(m-1)+m2-m=0.
解得m=-$\frac{4}{3}$或m=1.
经检验,当m=1时,△PQN不存在,故舍去m=1.
当m=-$\frac{4}{3}$时,所求直线l存在,且直线l的方程为y=x-$\frac{4}{3}$.
点评 本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式、三角形垂心的性质、相互垂直的直线斜率之间的关系、向量垂直与数量积的关系等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
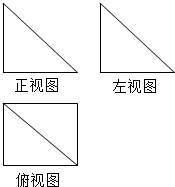 一个几何体的三视图如图所示,其中主视图和左视图是腰长为2的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是( )
一个几何体的三视图如图所示,其中主视图和左视图是腰长为2的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是( )| A. | 32$\sqrt{3}$π | B. | 4$\sqrt{3}$π | C. | 48π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
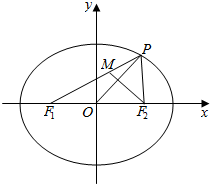 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1、F2,P是椭圆上一点,M在PF1上,且满足$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$(λ∈R),PO⊥F2M,O为坐标原点.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1、F2,P是椭圆上一点,M在PF1上,且满足$\overrightarrow{{F_1}M}=λ\overrightarrow{MP}$(λ∈R),PO⊥F2M,O为坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
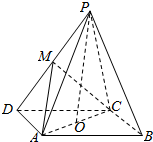 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,PO⊥平面ABCD,O点在AC上,PO=2,M为PD中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,PO⊥平面ABCD,O点在AC上,PO=2,M为PD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
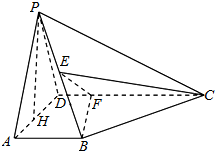 如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,E是PB的中点,F是CD上的点,PH为△PAD中AD边上的高.
如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,E是PB的中点,F是CD上的点,PH为△PAD中AD边上的高.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com