
分析 ①根据极值点的定义以及函数的定义进行判断.
②根据函数的奇偶性进行判断.
③根据导数和函数的单调性进行判断.
④判断函数的值域为R,进行判断.
解答 解:①∵f′(x0)=0,
∴x0是f(x)的极值点,
∴根据函数的定义和性质知f(x0)=0不一定成立,故①不正确;
②∵f(x)=x3+ax2+bx+c,
∴f(-x)=-x3+ax2-x+c≠-f(x)≠-f(x),
∴f(x)为非奇非偶函数,
∴f(x)不是轴对称图形,故②不正确;
③f′(x)=3x2+2ax+b,
当△=4a2-12b≤0时,f′(x)≥0恒成立,故f(x)单调递增函数,故③正确;
④∵函数f(x)的值域为R,
∴?x0∈R,使f(x0)=0,故④正确.
故正确的是③④,
故答案为:③④.
点评 本题考查命题的真假判断与应用,着重考查导函数与极值的应用,要求熟练掌握三次函数的图象和性质,属于中档题


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $6-\sqrt{2}$ | B. | $6+\sqrt{2}$ | C. | $5+\sqrt{2}$ | D. | $7+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
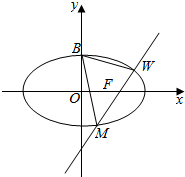 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,上顶点为B(0,1).
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,上顶点为B(0,1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
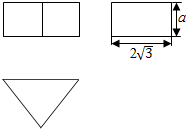
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
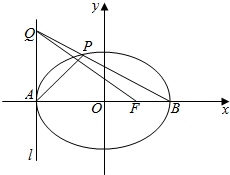 如图,A、B分别是椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(2>b>0)的左右顶点,F为其右焦点,|AF|×|FB|=3.
如图,A、B分别是椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(2>b>0)的左右顶点,F为其右焦点,|AF|×|FB|=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com