
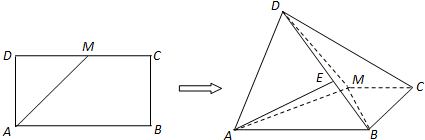
分析 (Ⅰ)由题意得AB=2,求得AM,BM的值,结合勾股定理可得MB⊥AM.再由面面垂直的性质可得BM⊥面ADM.从而得到AD⊥BM;
(Ⅱ)过D作DH⊥AM于H,在Rt△ADM中,可得DH.结合$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{DB}$,再由VD-AEM=VD-ABM-VE-ABM求解.
解答 (Ⅰ)证明:由题意得AB=2,$AM=BM=\sqrt{2}$,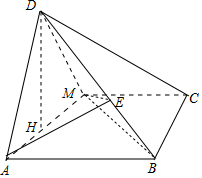
∴MB⊥AM.
又面ADM⊥面ABCM,面ADM∩ABCM=AM,BM?面ABCM,
∴BM⊥面ADM.
又AD?面ADM,
∴AD⊥BM;
(Ⅱ)由题意得${S}_{△ABM}=\frac{1}{2}$${S}_{长方形ABCD}=\frac{1}{2}×2×1=1$.
过D作DH⊥AM于H,在Rt△ADM中,可得DH=$\frac{\sqrt{2}}{2}$.
∵面ADM⊥面ABCM,∴DH⊥面ABCM.
∴${V}_{D-ABM}=\frac{1}{3}{S}_{△ABM}•DH=\frac{1}{3}×1×\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{6}$.
∵$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{DB}$,
∴VD-AEM=VD-ABM-VE-ABM=${V}_{D-ABM}-\frac{1}{3}•{S}_{△ABM}•\frac{1}{3}DH$
=$\frac{2}{3}{V}_{D-ABM}=\frac{2}{3}×\frac{\sqrt{2}}{6}=\frac{\sqrt{2}}{9}$.
点评 本题考查直线与平面垂直的判定与性质,考查了空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
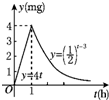 某医药研究所研发出一种新药,成年人按规定的剂量服用后,据检测,每毫升血液中的含药量y(mg)与时间t(h)之间的关系如图所示.据进一步测定,当每毫升血液中的含药量不少于0.25mg时,治疗疾病有效,则服药一次,治疗疾病有效的时间为( )
某医药研究所研发出一种新药,成年人按规定的剂量服用后,据检测,每毫升血液中的含药量y(mg)与时间t(h)之间的关系如图所示.据进一步测定,当每毫升血液中的含药量不少于0.25mg时,治疗疾病有效,则服药一次,治疗疾病有效的时间为( )| A. | 4 h | B. | 4$\frac{7}{8}$ h | C. | 4$\frac{15}{16}$ h | D. | 5 h |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,9] | B. | [$\frac{1}{3}$,9] | C. | [$\frac{1}{3}$,3] | D. | [$\frac{1}{9}$,$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1+a3≥2a2 | B. | 若a3>a1,则a4>a2 | C. | 若a1=a3,则a1=a2 | D. | a12+a32≥2a22 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com