练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．计算：（$\frac{1}{2}$）-2+log23•log3$\frac{1}{4}$=2．

    分析 直接利用指数、对数的运算性质化简求值．

    解答 解：原式=22+log23•$\frac{{log}_{2}\frac{1}{4}}{{log}_{2}3}$
    =4+log22-2=4-2=2，
    故答案为：2．

    点评 本题考查了指数、对数的运算性质，是基础的会考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．《九章算术》是我国古代的优秀数学著作，在人类历史上第一次提出负数的概率，内容涉及方程、几何、数列、面积、体积的计算等多方面，书的第6卷19题：“今有竹九节，下三节容量四升，上四节容量三升．”如果竹由下往上均匀变细（各节容量成等差数列），则其余两节的容量共多少升（　　）
    A．$1\frac{15}{66}$B．$1\frac{3}{22}$C．$2\frac{15}{66}$D．$2\frac{3}{22}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知函数g（x）=（a+1）x-2+1（a＞0）的图象恒过定点A，且点A又在函数$f（x）={log_{\sqrt{3}}}$（x+a）的图象上．
    （1）求实数a的值；
    （2）当方程|g（x+2）-2|=2b有两个不等实根时，求b的取值范围；
    （3）设an=g（n+2），bn=$\frac{{{a_n}-1}}{{{a_n}•{a_{n+1}}}}，n∈{N^*}$，求证：b1+b2+b3+…+bn＜$\frac{1}{3}$（n∈N*）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知，焦点在x轴上的椭圆的上下顶点分别为B2、B1，经过点B2的直线l与以椭圆的中心为顶点、以B2为焦点的抛物线交于A、B两点，直线l与椭圆交于B2、C两点，且|$\overrightarrow{A{B_2}}$|=2|$\overrightarrow{B{B_2}}$|．直线l1过点B1且垂直于y轴，线段AB的中点M到直线l1的距离为$\frac{9}{4}$．设$\overrightarrow{CB}$=λ$\overrightarrow{B{B_2}}$，则实数λ的取值范围是（　　）
    A．（0，3）B．（-$\frac{1}{2}$，2）C．（-$\frac{2}{3}$，4）D．（-$\frac{5}{9}$，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

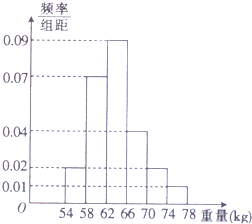
    3．为了了解某学校1200名高中男生的身体发育情况，抽查了该校100名高中男生的体重情况．根据所得数据画出样本的频率分布直方图，据此估计该校高中男生体重在66～79g的人数为（　　）
    A．360B．336C．300D．280

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．如图，已知长方形ABCD中，AB=2，AD=1，M为DC的中点． 将△ADM沿AM折起，使得平面ADM⊥平面ABCM．

    （Ⅰ）求证：AD⊥BM；
    （Ⅱ）若$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{DB}$时，求三棱锥D-AEM的体积．

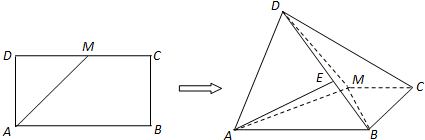
    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

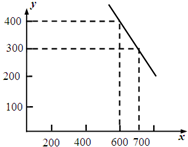    20．某公司试销一种成本单价为500元/件的新产品，规定试销时销售单价不低于成本单价，又不高于800元/件．经试销调查，发现销售量y（件）与销售单价x（元/件）可近似看作一次函数y=kx+b的关系（如图所示）．
    （1）由图象，求函数y=kx+b的表达式；
    （2）设公司获得的毛利润（毛利润=销售总价-成本总价）为S元．试用销售单价x表示毛利润S，并求销售单价定为多少时，该公司获得最大毛利润？最大毛利润是多少？此时的销售量是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．有一个公用电话亭，里面有一部电话，在观察使用这部电话的人的流量时，设在某一时刻，有n个人正在使用电话或等待使用的概率为P（n），且P（n）与时刻t无关，统计得到P（n）=$\left\{\begin{array}{l}{（\frac{1}{2}）^{n}•P（0），1≤n≤6}\\{0，n≥7}\end{array}\right.$，那么在某一时刻，这个公用电话亭里一个人也没有的概率P（0）的值是$\frac{64}{127}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知幂函数f（x）=xn的图象过点（8，$\frac{1}{4}$），且f（a+1）＜f（2），则a的范围是（　　）
    A．-3＜a＜1B．a＜-3或a＞1C．a＜1D．a＞1

    查看答案和解析>>

    同步练习册答案