
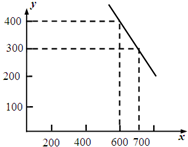
 某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).
某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).分析 (1)把点(700,300)和点(600,400)分别代入一次函数y=kx+b,解方程组求得k和b的值,即可得到一次函数y=kx+b的表达式.
(2)由题意可得 S=y•x-500y,化简可得S=-x2+1500x-500000,利用二次函数性质求出函数的最大值以及函数取最大值时x的值.
解答 解:(1)把点(700,300)和点(600,400)分别代入一次函数y=kx+b
可得 300=700k+b,且400=600k+b,
解得 k=-1,b=1000,
故一次函数y=kx+b的表达式为 y=-x+1000(500≤x≤800). 6分
(2)∵公司获得的毛利润(毛利润=销售总价-成本总价)为S,
则S=y•x-500y=(-x+1000 )x-500(-x+1000)=-x2+1500x-500000.
故函数S的对称轴为x=750,满足500≤x≤800,故当x=750时,函数S取得最大值为62500元,
即当销售单价定为750元/价时,该公司可获得最大的毛利润为62500元,此时y=250. 14分.
点评 本题主要考查用待定系数法求直线方程,二次函数性质的应用,体现了数形结合的数学思想,属于中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:解答题
 如图,已知△ABC中,D为BC的中点,AE=$\frac{1}{2}$EC,AD,BE交于点F,设$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图,已知△ABC中,D为BC的中点,AE=$\frac{1}{2}$EC,AD,BE交于点F,设$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
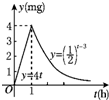 某医药研究所研发出一种新药,成年人按规定的剂量服用后,据检测,每毫升血液中的含药量y(mg)与时间t(h)之间的关系如图所示.据进一步测定,当每毫升血液中的含药量不少于0.25mg时,治疗疾病有效,则服药一次,治疗疾病有效的时间为( )
某医药研究所研发出一种新药,成年人按规定的剂量服用后,据检测,每毫升血液中的含药量y(mg)与时间t(h)之间的关系如图所示.据进一步测定,当每毫升血液中的含药量不少于0.25mg时,治疗疾病有效,则服药一次,治疗疾病有效的时间为( )| A. | 4 h | B. | 4$\frac{7}{8}$ h | C. | 4$\frac{15}{16}$ h | D. | 5 h |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com