
分析 首先设三角形的边长为4,并以BC为横轴,BC的中垂线为纵轴建立坐标系,进而写出A、B、C、D、E的坐标,然后根据双曲线的定义得出a的值,即可求出结果.
解答 解:以BC为横轴,BC的中垂线为纵轴,设B(-2,0)C(2,0)
则A(0,2$\sqrt{3}$),D(-1,$\sqrt{3}$),E(1,$\sqrt{3}$),c=2,
∵椭圆与双曲线均过D,E,
∴2a=BE-CE=2($\sqrt{3}$-1),
∴a=$\sqrt{3}$-1,
∴e=$\frac{2}{\sqrt{3}-1}$=$\sqrt{3}$+1.
故答案为$\sqrt{3}$+1.
点评 本题考查了双曲线的定义以及性质,对于选择题与填空题可以采取灵活多样的方法作答,其中取特殊值法是常用方法.


科目:高中数学 来源: 题型:选择题
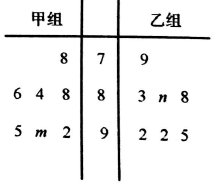 某中学奥数培训班共有14人,分为两个小组,在一次阶段测试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则n-m的值( )
某中学奥数培训班共有14人,分为两个小组,在一次阶段测试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则n-m的值( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $1\frac{15}{66}$ | B. | $1\frac{3}{22}$ | C. | $2\frac{15}{66}$ | D. | $2\frac{3}{22}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{12}$ | D. | $\frac{7π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
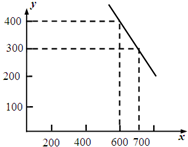 某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).
某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com