
分析 有题意:直线mx-y-2m-1=0(m∈R)与点(-2,3)为圆心的圆相切,所有的圆中,圆心到直线的定点的距离为半径的圆最大,从而可以求解得圆的标准方程.
解答 解:有题意:以点(-2,3)为圆心且与直线mx-y-2m-1=0(m∈R)相切的所有圆中,半径最大,即是圆心到直线的定点的距离为半径的圆最大.
直线mx-y-2m-1=0(m∈R),恒过(0,-1),
那么:${r}_{max}=\sqrt{(0+2)^{2}(3+1)^{2}}=\sqrt{20}$.
所以半径最大的圆的标准方程(x+2)2+(y-3)2=20.
故答案为:(x+2)2+(y-3)2=20.
点评 本题考了直线过定点的问题和圆与直线的位置关系的运用.属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n-1 | B. | ($\frac{3}{2}$)n-1 | ||
| C. | ($\frac{2}{3}$)n-1 | D. | $\left\{\begin{array}{l}{1,n=1}\\{\frac{1}{2}{•(\frac{3}{2})}^{n-2},n≥2}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cos2x,x∈R | B. | y=$\frac{{e}^{x}-{e}^{-x}}{2}$,x∈R | C. | y=$sin|\frac{x}{2}|$,x?R | D. | y=x3+x,x?R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
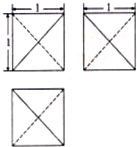
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com