
| A. | a>b>c>d | B. | b>a>c>d | C. | d>a>b>c | D. | a>d>c>b |
分析 求出函数的导数,利用导函数的符号判断函数的单调性,然后判断函数值的大小.
解答 解:函数f(x)=(2x-1)ex,可得f′(x)=(2x+1)ex,
当x<-$\frac{1}{2}$时,f′(x)<0,函数是减函数,
∵ln$\sqrt{e}$<ln2<lne,∴$\frac{1}{2}<ln2<1$$<\sqrt{2}$,
∴$-\sqrt{2}<-1<-ln2<-\frac{1}{2}$,
∴f(-$\sqrt{2}$)>f(-ln2)>f(-$\frac{1}{2}$),
∵f(1)>0,f($-\sqrt{2}$)<0,
∴a>b>c>d.
故选:A.
点评 本题考查函数的导数的应用,函数的单调性的判断与应用,是基础题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | y=x4+2x | B. | y=2|x| | C. | y=2x-2-x | D. | $y={log_{\frac{1}{2}}}|x|-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?p | B. | q | C. | p∨(?q) | D. | (?p)∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?m∈[{0,1}],x+\frac{1}{x}<{2^m}$ | B. | $?m∈[{0,1}],x+\frac{1}{x}≥{2^m}$ | C. | $?m∈[{0,1}],x+\frac{1}{x}≤{2^m}$ | D. | $?m∈[{0,1}],x+\frac{1}{x}<{2^m}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
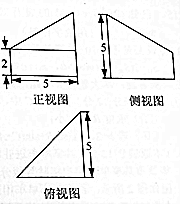 《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱,已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( )
《九章算术》是中国古代第一部数学专著,书中有关于“堑堵”的记载,“堑堵”即底面是直角三角形的直三棱柱,已知某“堑堵”被一个平面截去一部分后,剩下部分的三视图如图所示,则剩下部分的体积是( )| A. | 50 | B. | 75 | C. | 25.5 | D. | 37.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
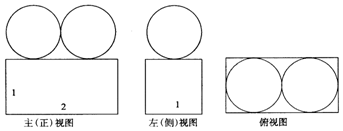
| A. | 2+$\frac{4π}{3}$ | B. | 2+$\frac{π}{3}$ | C. | 1+$\frac{4π}{3}$ | D. | 10+8π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 数据 | 31,12,22,15,20,45,47,32,34,23,28 |
| A. | 23、32 | B. | 34、35 | C. | 28、32 | D. | 28、35 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$| | B. | $\frac{1}{2}$$|\begin{array}{l}{{x}_{1}}&{{y}_{1}}&{1}\\{{x}_{2}}&{{y}_{2}}&{1}\\{{x}_{3}}&{{y}_{3}}&{1}\end{array}|$ | ||
| C. | $\frac{1}{2}$|$\overrightarrow{AB}$$•\overrightarrow{AC}$| | D. | $\frac{1}{2}$(cos|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com