Question

10．椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）上一点A关于原点的对称点为B，F为其右焦点，若AF⊥BF，设∠ABF=α，且α∈[$\frac{π}{12}$，$\frac{π}{4}$]，则该椭圆离心率的最大值为（　　）

• A． $\frac{{\sqrt{6}}}{3}$
• B． $\frac{{\sqrt{3}}}{2}$
• C． $\frac{{\sqrt{2}}}{2}$
• D． 1

Answer 1

分析 由椭圆的焦点在x轴上，设左焦点为F₁，根据椭圆的定义：|AF|+|AF₁|=2a，∠ABF=α，则：∠AF₁F=α．则2a=2ccosα+2csinα，即a=（cosα+sinα）c，由椭圆的离心率e=$\frac{c}{a}$=$\frac{1}{sinα+cosα}$=$\frac{1}{\sqrt{2}sin（α+\frac{π}{4}）}$，由α∈[$\frac{π}{12}$，$\frac{π}{4}$]，根据正弦函数的图象及性质，求得椭圆离心率的取值范围，即可求得椭圆离心率的最大值．

解答 解：已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）焦点在x轴上，
椭圆上一点A关于原点的对称点为点B，F为其右焦点，设左焦点为F₁，
则：连接AF，AF₁，AF，BF
所以：四边形AFF₁B为长方形．
根据椭圆的定义：|AF|+|AF₁|=2a，
∠ABF=α，则：∠AF₁F=α．
∴2a=2ccosα+2csinα，即a=（cosα+sinα）c，
由椭圆的离心率e=$\frac{c}{a}$=$\frac{1}{sinα+cosα}$=$\frac{1}{\sqrt{2}sin（α+\frac{π}{4}）}$，
由α∈[$\frac{π}{12}$，$\frac{π}{4}$]，
α+$\frac{π}{4}$∈[$\frac{π}{3}$，$\frac{π}{2}$]，
sin（α+$\frac{π}{4}$）∈[$\frac{\sqrt{3}}{2}$，1]，
$\sqrt{2}$sin（α+$\frac{π}{4}$）∈[$\frac{\sqrt{6}}{2}$，$\sqrt{2}$]，
$\frac{1}{\sqrt{2}sin（α+\frac{π}{4}）}$∈[$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{6}}{3}$]，
∴e∈[$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{6}}{3}$]，
故椭圆离心率的最大值$\frac{\sqrt{6}}{3}$．
故选A．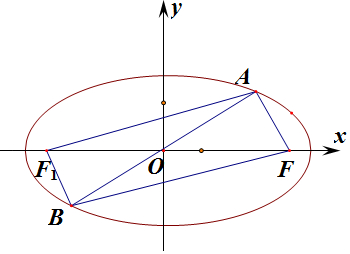

点评 本题考查了椭圆的定义及其性质、两角差的正弦公式、正弦函数的单调性，考查了推理能力与计算能力，属于难题．