
| 组别 | 文科 | 理科 | ||
| 性别 | 男生 | 女生 | 男生 | 女生 |
| 人数 | 3 | 1 | 3 | 2 |
分析 (Ⅰ)基本事件总数:n=${C}_{4}^{1}{C}_{5}^{3}+{C}_{4}^{2}{C}_{5}^{2}$+${C}_{4}^{3}{C}_{5}^{1}$=120,“理科组恰好得4分“的选法有两种情况:①从理科组中选取2男1女,再从文科组任选1人;②从理科组中选2名女生,再从文科组中任选2人.由此能求出理科组恰好得4分的概率.
(II)由题意知,文科组得分X的取值为1,2,3,4,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)∵被选出的4人中文科组和理科组的学生都有,
∴基本事件总数:n=${C}_{4}^{1}{C}_{5}^{3}+{C}_{4}^{2}{C}_{5}^{2}$+${C}_{4}^{3}{C}_{5}^{1}$=120,
“理科组恰好得4分“的选法有两种情况:
①从理科组中选取2男1女,再从文科组任选1人,共有:${C}_{3}^{2}{C}_{2}^{1}{C}_{4}^{1}$=24种选法,
②从理科组中选2名女生,再从文科组中任选2人,共有:${C}_{2}^{2}{C}_{4}^{2}=6$种选法,
∴理科组恰好得4分的概率p=$\frac{24+6}{120}$=$\frac{1}{4}$.
(II)由题意知,文科组得分X的取值为1,2,3,4,
P(X=1)=$\frac{{C}_{3}^{1}{C}_{5}^{3}}{120}$=$\frac{3×10}{120}$=$\frac{1}{4}$,
P(X=2)=$\frac{{C}_{3}^{2}{C}_{5}^{2}+{C}_{1}^{1}{C}_{5}^{3}}{120}$=$\frac{3×10+10}{120}$=$\frac{1}{3}$,
P(X=3)=$\frac{{C}_{3}^{3}{C}_{5}^{1}+{C}_{3}^{1}{C}_{1}^{1}{C}_{5}^{2}}{120}=\frac{5+3×10}{120}$=$\frac{7}{24}$,
P(X=4)=$\frac{{C}_{3}^{2}{C}_{1}^{1}{C}_{5}^{1}}{120}=\frac{1}{8}$,
∴X的分布列为:
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{7}{24}$ | $\frac{1}{8}$ |
点评 本题考查离散型随机变量的分布列、数学期望等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 已知命题p,q,若p∨(¬q)为真命题,则q一定是假命题 | |
| B. | 命题“?x∈R,2x>0”的否定是“$?{x_0}∈R,{2^{x_0}}<0$” | |
| C. | “$x=\frac{π}{4}$”是“tan x=l”的充分不必要条件 | |
| D. | “若x1>1,x2>1,则x1+x2>2”的否命题是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
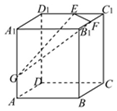 如图所示,在正方体ABCD-A1B1C1D1中,点G在棱AA1上,AG=$\frac{1}{3}$AA1,E,F分别是棱
如图所示,在正方体ABCD-A1B1C1D1中,点G在棱AA1上,AG=$\frac{1}{3}$AA1,E,F分别是棱| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
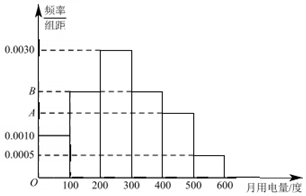 某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费.超过200度但不超过400度的部分按0.8 元/度收费,超过400度的部分按1.0 元/度收费.
某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费.超过200度但不超过400度的部分按0.8 元/度收费,超过400度的部分按1.0 元/度收费.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com