
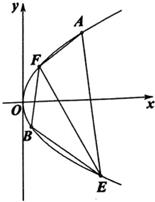
 如图,A(1,2)、B($\frac{1}{4}$,-1)是抛物线y2=ax(a>0)上的两个点,过点A、B引抛物线的两条弦AE,BF.
如图,A(1,2)、B($\frac{1}{4}$,-1)是抛物线y2=ax(a>0)上的两个点,过点A、B引抛物线的两条弦AE,BF.分析 (1)把A(1,2)代入抛物线y2=ax(a>0),即可解出a.
(2)(i)设直线AE的方程为:y-2=k(x-1),化为:y=kx+2-k,(k≠0),则直线BF的方程为:y+1=-k(x-$\frac{1}{4}$),化为:y=-kx+$\frac{k}{4}$-1.分别与抛物线方程联立即可得出kEF=-1为定值.
(ii)设直线EF的方程为:y=-x+t,与抛物线方程联立化为:y2+4y-4t=0,△>0,解得t>-1.可得|EF|=$\sqrt{2[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$,点A到直线EF的距离d1,点B到直线EF的距离d2.四边形AEBF面积S=$\frac{1}{2}|EF|$(d1+d2)=$\frac{1}{2}$$\sqrt{1+t}$(4|t-3|+|4t+3|).对t分类讨论,利用单调性即可得出.
解答 解:(1)把A(1,2)代入抛物线y2=ax(a>0),可得:22=a,解得a=4.
(2)(i)设直线AE的方程为:y-2=k(x-1),化为:y=kx+2-k,(k≠0),
则直线BF的方程为:y+1=-k(x-$\frac{1}{4}$),化为:y=-kx+$\frac{k}{4}$-1.
联立$\left\{\begin{array}{l}{y=kx+2-k}\\{{y}^{2}=4x}\end{array}\right.$,化为ky2-4y+8-4k=0,∴2yE=$\frac{8-4k}{k}$,
解得yE=$\frac{4-2k}{k}$,∴xE=$\frac{{k}^{2}-4k+4}{{k}^{2}}$.∴E$(\frac{{k}^{2}-4k+4}{{k}^{2}},\frac{4-2k}{k})$.
联立$\left\{\begin{array}{l}{y=-kx+\frac{k}{4}-1}\\{{y}^{2}=4x}\end{array}\right.$,化为:ky2+4y+4-k=0,
∴-yF=$\frac{4-k}{k}$,可得yF=$\frac{k-4}{k}$,解得xF=$\frac{{k}^{2}-8k+16}{4{k}^{2}}$.
∴F$(\frac{{k}^{2}-8k+16}{4{k}^{2}},\frac{k-4}{k})$,
∴kEF=$\frac{\frac{k-4}{k}-\frac{4-2k}{k}}{\frac{{k}^{2}-8k+16}{4{k}^{2}}-\frac{{k}^{2}-4k+4}{{k}^{2}}}$=-4为定值.
(ii)设直线EF的方程为:y=-x+t,
联立$\left\{\begin{array}{l}{y=-x+t}\\{{y}^{2}=4x}\end{array}\right.$,化为:y2+4y-4t=0,
△=16+16t>0,解得t>-1.
∴y1+y2=-4,y1y2=-4t.
∴|EF|=$\sqrt{2[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$=$\sqrt{2(16+16t)}$=4$\sqrt{2(1+t)}$.
点A到直线EF的距离d1=$\frac{|1+2-t|}{\sqrt{2}}$=$\frac{|3-t|}{\sqrt{2}}$,
点B到直线EF的距离d2=$\frac{|\frac{1}{4}-1-t|}{\sqrt{2}}$=$\frac{|4t+3|}{4\sqrt{2}}$.
∴四边形AEBF面积S=$\frac{1}{2}|EF|$(d1+d2)
=$\frac{1}{2}×$4$\sqrt{2(1+t)}$×$\frac{4|t-3|+|4t+3|}{4\sqrt{2}}$=$\frac{1}{2}$$\sqrt{1+t}$(4|t-3|+|4t+3|).
①t≥3时,S=$\frac{1}{2}\sqrt{1+t}$(4t-12+4t+3)=$\frac{1}{2}\sqrt{1+t}$(8t-9)≥$\frac{1}{2}×\sqrt{1+3}×(24-9)$=15.
②$-\frac{3}{4}$≤t<3时,S=$\frac{1}{2}\sqrt{1+t}$(-4t+12+4t+3)=$\frac{1}{2}\sqrt{1+t}$×15∈$[\frac{15}{4},15)$.
②-1<t<$-\frac{3}{4}$时,S=$\frac{1}{2}\sqrt{1+t}$(-4t+12-4t-3)=$\frac{1}{2}\sqrt{1+t}$×(9-8t),
令g(t)=$\frac{1}{4}(1+t)(9-8t)^{2}$=16t3-20t2-$\frac{63}{4}$t+$\frac{81}{4}$.
g′(t)=48t2-40t-$\frac{63}{4}$,对称轴为t=$\frac{5}{12}$,函数g′(t)在$(-1,-\frac{3}{4})$上单调递减,
而${g}^{′}(-\frac{3}{4})$=9+30-$\frac{63}{4}$>0,∴函数g(t)在$(-1,-\frac{3}{4})$上单调递增,
∴S在$(-1,-\frac{3}{4})$上单调递增.
∴S∈$(0,\frac{15}{4})$.
综上可得:S∈(0,15).
点评 本题考查了抛物线的标准方程及其性质、直线与抛物线相交弦长问题、一元二次方程的根与系数的关系、点到直线的距离公式、利用导数研究函数的单调性极值与最值,考查了分析问题与解决问题的能力、推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
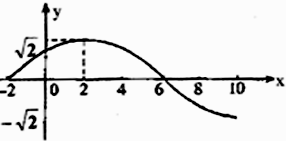 已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示:
已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 965 | B. | 975 | C. | 985 | D. | 995 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 模型1的相关指数R2为0.87 | B. | 模型2的相关指数R2为0.97 | ||
| C. | 模型3的相关指数R2为0.50 | D. | 模型4的相关指数R2为0.25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com