
分析 (1)分别用$\overrightarrow{OA}$,$\overrightarrow{OB}$来表示$\overrightarrow{DE}$,$\overrightarrow{OD}$,证明$\overrightarrow{DE},\overrightarrow{OD}$存在倍数关系即可;
(2)作出平面图形,根据平面向量的加法法则推出两个三角形高的关系.
解答 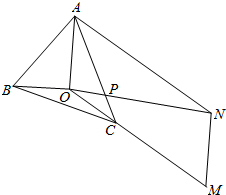 解:(1)∵$\overrightarrow{OA}$+2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=0,∴$\overrightarrow{OC}$=-$\frac{1}{3}$($\overrightarrow{OA}$+2$\overrightarrow{OB}$)=-$\frac{1}{3}$$\overrightarrow{OA}$-$\frac{2}{3}\overrightarrow{OB}$,
解:(1)∵$\overrightarrow{OA}$+2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=0,∴$\overrightarrow{OC}$=-$\frac{1}{3}$($\overrightarrow{OA}$+2$\overrightarrow{OB}$)=-$\frac{1}{3}$$\overrightarrow{OA}$-$\frac{2}{3}\overrightarrow{OB}$,
∵D是BC中点,∴$\overrightarrow{OD}$=$\frac{1}{2}$($\overrightarrow{OB}$+$\overrightarrow{OC}$)=$\frac{1}{2}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$=$\frac{1}{6}$$\overrightarrow{OB}$-$\frac{1}{6}$$\overrightarrow{OA}$,
$\overrightarrow{DE}$=$\frac{1}{2}\overrightarrow{BA}$=$\frac{1}{2}$($\overrightarrow{OA}-\overrightarrow{OB}$),
∴$\overrightarrow{DE}$=-3$\overrightarrow{OD}$,∴D,E,O共线.
(2)延长OC至M点,使得OM=3OC,以OA,OM为邻边作平行四边形OANM,
则$\overrightarrow{OA}+3\overrightarrow{OC}$=$\overrightarrow{ON}$,∵$\overrightarrow{OA}$+3$\overrightarrow{OC}$=-2$\overrightarrow{OB}$,
∴$\overrightarrow{ON}$=-2$\overrightarrow{OB}$,
∵OM=3OC,∴ON=4OP,
∴OP=$\frac{1}{2}OB$=$\frac{1}{3}$BP,
∴$\frac{{S}_{△ABC}}{{S}_{△AOC}}$=$\frac{BP}{OP}$=3.
点评 本题考查了平面向量线性运算的性质,正确画出图形并找到线段的关系是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f({0.7^6})<f({log_{0.7}}6)<f({6^{0.5}})$ | B. | f(0.76)<f(60.5)<f(log0.76) | ||
| C. | $f({log_{0.7}}6)<f({0.7^6})<f({6^{0.5}})$ | D. | $f({log_{0.7}}6)<f({6^{0.5}})<f({0.7^6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|-1<a<3} | B. | {a|-2<a<4} | C. | {a|-2≤a≤4} | D. | {a|-1≤a≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
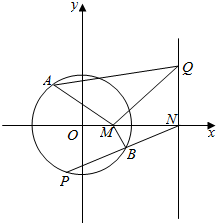 如图,自点M(1,0)引直线交椭圆$\frac{{x}^{2}}{4}$+y2=1于A,B两点,直线l:x=4与x轴交于点N,设点A关于x轴的对称点为P(异于点B).
如图,自点M(1,0)引直线交椭圆$\frac{{x}^{2}}{4}$+y2=1于A,B两点,直线l:x=4与x轴交于点N,设点A关于x轴的对称点为P(异于点B).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{15}{4}$ | D. | $\frac{15}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5$\sqrt{2}$ | B. | 4$\sqrt{2}$-1 | C. | 6$\sqrt{2}$-1 | D. | $\sqrt{61}$-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com