
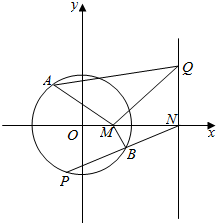
 如图,自点M(1,0)引直线交椭圆$\frac{{x}^{2}}{4}$+y2=1于A,B两点,直线l:x=4与x轴交于点N,设点A关于x轴的对称点为P(异于点B).
如图,自点M(1,0)引直线交椭圆$\frac{{x}^{2}}{4}$+y2=1于A,B两点,直线l:x=4与x轴交于点N,设点A关于x轴的对称点为P(异于点B).分析 (1)设B(x1,y1),A(x2,y2),P(x2,-y2),l:y=k(x-1),代入椭圆方程,利用韦达定理,结合BP的方程为y-y1=$\frac{{y}_{1}+{y}_{2}}{{x}_{1}-{x}_{2}}$(x-x1),令y=0,化简求解可得x=4,即可证明P、B、N三点共线;
(2)分别求出S1、S2、S3,可得λ=$\frac{{{S}_{2}}^{2}}{{S}_{1}{S}_{3}}$=$\frac{12|k|{{y}_{2}}^{2}}{|3k-2{y}_{2}||{y}_{1}{y}_{2}|}$,结合韦达定理,即可得出结论.
解答 (1)证明:设B(x1,y1),A(x2,y2),P(x2,-y2),l:y=k(x-1),
代入$\frac{{x}^{2}}{4}$+y2=1整理得(1+4k2)x2-8k2x+4k2-4=0,
由韦达定理可得:x1+x2=$\frac{8{k}^{2}}{1+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}-4}{1+4{k}^{2}}$
BP的方程为y-y1=$\frac{{y}_{1}+{y}_{2}}{{x}_{1}-{x}_{2}}$(x-x1)
令y=0,得x=$\frac{2{x}_{1}{x}_{2}-({x}_{1}+{x}_{2})}{{x}_{1}+{x}_{2}-2}$=4.
∴直线BP过定点N(4,0),
∴P、B、N三点共线;
(2)解:Q(4,y0),
∵AQ∥PB,∴$\frac{{y}_{0}-{y}_{2}}{4-{x}_{2}}$=$\frac{{y}_{2}}{4-{x}_{2}}$,
∴y0=2y2,|AM|=$\sqrt{({x}_{2}-1)^{2}+{{y}_{2}}^{2}}$=$\frac{\sqrt{1+{k}^{2}}|{y}_{2}|}{|k|}$,
∵Q到直线AM:kx-y-k=0的距离d=$\frac{|3k-2{y}_{2}|}{\sqrt{1+{k}^{2}}}$,
∴S1=$\frac{1}{2}|AM|d$=$\frac{|3k-2{y}_{2}||{y}_{2}|}{2|k|}$,S2=$\frac{1}{2}|MN||{y}_{0}|$=3|y2|,S3=$\frac{1}{2}|MN||{y}_{2}|$=$\frac{3}{2}$|y2|,
∴λ=$\frac{{{S}_{2}}^{2}}{{S}_{1}{S}_{3}}$=$\frac{12|k|{{y}_{2}}^{2}}{|3k-2{y}_{2}||{y}_{1}{y}_{2}|}$,
∵y1y2=k(x1-1)•k(x2-1)=$\frac{-3{k}^{2}}{4{k}^{2}+1}$,y1+y2=$\frac{-2k}{4{k}^{2}+1}$,
∴2y1y2=3(y1+y2),3k-2y2=-$\frac{2{{y}_{2}}^{2}}{{y}_{1}+{y}_{2}}$,
∴λ=$\frac{6|k({y}_{1}+{y}_{2}\}|}{|{y}_{1}{y}_{2}|}$=4,
∴存在λ=4,使得S22=λS1S3.
点评 本题考查椭圆方程的求法,直线与椭圆的位置关系的应用,考查转化思想以及计算能力,属于中档题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
 如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离为12nmile,在A处看灯塔C在货轮的北偏西30°,距离为8nmile,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:
如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离为12nmile,在A处看灯塔C在货轮的北偏西30°,距离为8nmile,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
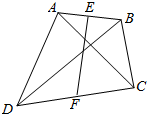 已知,如图所示,点E、F分别为任意四边形ABCD对边AB、CD的中点,求证:$\overrightarrow{EF}$=$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{BD}$).
已知,如图所示,点E、F分别为任意四边形ABCD对边AB、CD的中点,求证:$\overrightarrow{EF}$=$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{BD}$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com